题目内容

如图，一边靠校园围墙，其他三边用总长为40米的铁栏杆围成一个矩形花圃，设矩形ABCD的边AB为x米，面积为S平方米，要使矩形ABCD面积最大，则x的长为（　　）
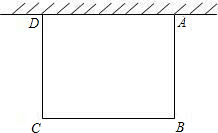
A．10米B．15米C．20米D．25米

设矩形ABCD的边AB为x米，则宽为40-2x，
S=（40-2x）x=-2x2+40x．
要使矩形ABCD面积最大，
则x=-
b
2a
=-
40
(-2)×2
=10m，
即x的长为10m．
故选A．
练习册系列答案
相关题目
如图1，已知抛物线的顶点为A（2，1），且经过原点O，与x轴的另一个交点为B．
（1）求抛物线的解析式；
（2）若点C在抛物线的对称轴上，点D在抛物线上，且以O、C、D、B四点为顶点的四边形为平行四边形，求D点的坐标；
（3）连接OA、AB，如图2，在x轴下方的抛物线上是否存在点P，使得△OBP与△OAB相似？若存在，求出P点的坐标；若不存在，说明理由．
如图是一个抛物线形拱桥的示意图，桥的跨度AB为100米，支撑桥的是一些等距的立柱，相邻立柱的水平距离为10米（不考虑立柱的粗细），其中距A点10米处的立柱FE的高度为3.6米．
（1）求正中间的立柱OC的高度；
（2）是否存在一根立柱，其高度恰好是OC的一半？请说明理由．
已知如图抛物线l1与x轴的交点的坐标为（-1，0）和（-5，0），与y轴的交点坐标为（0，2.5）．
（1）求抛物线l1的解析式；
（2）抛物线l2与抛物线l1关于原点对称，现有一身高为1.5米的人撑着伞与抛物线l2的对称轴重合，伞面弧AB与抛物线l2重合，头顶最高点C与伞的下沿AB在同一条直线上（如图所示不考虑其他因素），如果雨滴下降的轨迹是沿着直线y=mx+b运动，那么不被淋到雨的m的取值范围是多少？
（3）将伞的下沿AB沿着抛物线l2对称轴上升10厘米至A1B1，A1B1比AB长8厘米，抛物线l2除顶点M不动外仍经过弧A1B1（其余条件不变），那么被雨淋到的几率是扩大了还是缩小了，说明理由．
已知二次函数y=ax2+bx+c的图象过点A（2，4），顶点的横坐标为
1
2
，它的图象与x轴交于两点B（x1，0）、C（x2，0），与y轴交于点D，且x12+x22=13．试问：y轴上是否存在点P，使得△POB与△DOC相似（O为坐标原点）？若存在，请求出过P、B两点直线的解析式；若不存在，请说明理由．
如图所示，已知抛物线y=ax2+bx+c过点A（-1，0），且经过直线y=x-3与坐标轴的两个交点B、C．
（1）求抛物线的表达式；
（2）若点M在第四象限内且在抛物线上，有OM⊥BC，垂足为D，求点M的坐标．
如图，抛物线y=ax2+bx-4与x轴交于A（-4，0）、B（3，0）两点，与y轴交于点C．

（1）求抛物线的函数关系式；
（2）点P是抛物上第三象限内的一动点，当点P运动到什么位置时，四边形ABCP的面积最大？求出此时点P的坐标和四边形ABCP的面积；
（3）点M在抛物线对称轴上，点N是平面内一点，是否存在这样的点M、N，使得以点M、N、B、C为顶点的四边形是菱形？若存在，请直接写出点M的坐标；若不存在，请说明理由．
如图，已知一动圆的圆心P在抛物线y=
1
2
x2-3x+3上运动．若⊙P半径为1，点P的坐标为（m，n），当⊙P与x轴相交时，点P的横坐标m的取值范围是______．
如图，平行于x轴的直线AC分别交抛物线y1=x2（x≥0）与y2=
x2
3
（x≥0）于B、C两点，过点C作y轴的平行线交y1于点D，直线DE∥AC，交y2于点E，则
DE
AB
=______．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网