Question

【题目】在中，点是直线上的一动点(不与点重合)，连接在的右侧以为斜边作等腰直角三角形.点是的中点，连接.

[问题发现]

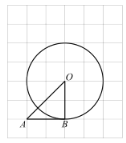
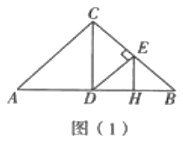
（1）如图(1)，当点是的中点时，线段与的数量关系是______，与的位置关系是______；

　

[猜想论证]

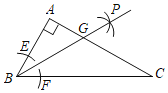
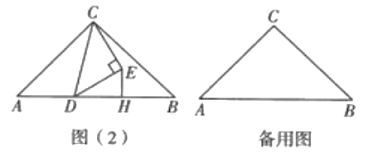
（2）如图（2），当点在边上且不是的中点时，(1)中的结论是否仍然成立？若成立，请仅就图（2）中的情况给出证明；若不成立，请说明理由．

[拓展应用]

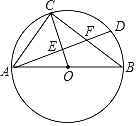
（3）若，其他条件不变，连接.当是等边三角形时，请直接写出的面积．

Answer 1

【答案】（1）；（2）仍然成立，证明见解析；（3）的面积是或．

【解析】

（1）利用等腰直角三角形的判定和性质解决问题即可．
（2）结论仍然成立：如图2中，延长DE到F，使得EF＝DE，连接CF，BF．证明△ACD≌△BCF（SAS），再利用三角形的中位线定理即可解决问题．
（3）分两种情形：如图3-1中，当△BCE是等边三角形时，过点E作EH⊥BD于H．如图32中，当△BCE是等边三角形时，过点E作EH⊥BD于H．分别求出AD，EH即可解决问题．

（1）如图1中，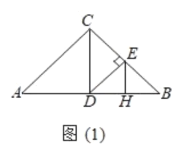

∵CA＝CB，∠ACB＝90°，AD＝BD，
∴CD⊥AB，CD＝AD＝DB，
∴∠A＝∠B＝45°，∠DCB＝∠ACD＝45°，
∵∠DCE＝45°，
∴点E在线段CB上，
∵DE⊥BC，
∴∠EDB＝∠B＝45°，
∵DH＝HB，
∴EH⊥DB，EH＝DB＝AD，
故答案为：EH＝AD，EH⊥AD．

（2）仍然成立

如图，延长到，使得连接

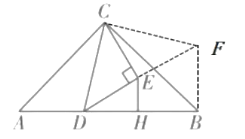
则垂直平分线段.

.

在和中，

点分别是和的中点，

是的中位线，

且

（3）如图31中，当△BCE是等边三角形时，过点E作EH⊥BD于H．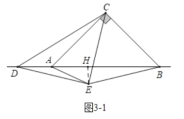

∵∠ACB＝90°，∠ECB＝60°，
∴∠ACE＝30°，
∵AC＝CB＝CE＝EB＝DE＝，
∴∠CAE＝∠CEA＝75°，
∵∠CAB＝45°，
∴∠EAH＝30°，
∵∠DEC＝90°，∠CEB＝60°，
∴∠DEB＝150°，
∴∠EDB＝∠EBD＝15°，
∵∠EAH＝∠ADE＋∠AED，
∴∠ADE＝∠AED＝15°，
∴AD＝AE，设EH＝x，则AD＝AE＝2x，AH＝，
∵EH＋DH＝DE，
∴

∴x＝，
∴AD＝，

∴S△ADE＝=，

如图32中，当△BCE是等边三角形时，过点E作EH⊥BD于H．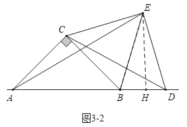

同法可求：EH＝，AD＝，

∴S△ADE＝,

综上所述，满足条件的△ADE的面积为42或4＋2．