Question

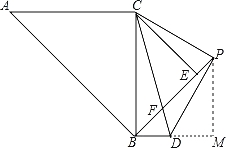
【题目】如图，△ABC和△BEC均为等腰直角三角形，且∠ACB=∠BEC=90°，AC=4，点P为线段BE延长线上一点，连接CP以CP为直角边向下作等腰直角△CPD，线段BE与CD相交于点F

（1）求证：；

（2）连接BD，请你判断AC与BD有什么位置关系？并说明理由；

（3）设PE=x，△PBD的面积为S，求S与x之间的函数关系式．

Answer 1

【答案】（1）证明过程见解析；（2）AC∥BD；理由见解析；（3）S=x2+2x

【解析】

试题分析：（1）直接利用相似三角形的判定方法得出△BCE∽△DCP，进而得出答案；（2）首先得出△PCE∽△DCB，进而求出∠ACB=∠CBD，即可得出AC与BD的位置关系；（3）首先利用相似三角形的性质表示出BD，PM的长，进而表示出△PBD的面积．

试题解析：（1）∵△BCE和△CDP均为等腰直角三角形， ∴∠ECB=∠PCD=45°，∠CEB=∠CPD=90°，

∴△BCE∽△DCP， ∴=；

（2）AC∥BD，

理由：∵∠PCE+∠ECD=∠BCD+∠ECD=45°， ∴∠PCE=∠BCD， 又∵=， ∴△PCE∽△DCB，

∴∠CBD=∠CEP=90°， ∵∠ACB=90°， ∴∠ACB=∠CBD， ∴AC∥BD；

（3）如图所示：作PM⊥BD于M， ∵AC=4，△ABC和△BEC均为等腰直角三角形， ∴BE=CE=4，

∵△PCE∽△DCB， ∴=，即=， ∴BD=x，

∵∠PBM=∠CBD﹣∠CBP=45°，BP=BE+PE=4+x， ∴PM=，

∴△PBD的面积S=BDPM=×x×=x2+2x．