题目内容
【题目】如图，抛物线y=ax2+bx﹣5（a≠0）与x轴交于点A（﹣5，0）和点B（3，0），与y轴交于点C．
（1）求该抛物线的解析式；
（2）若点E为x轴下方抛物线上的一动点，当S△ABE=S△ABC时，求点E的坐标；
（3）在（2）的条件下，抛物线上是否存在点P，使∠BAP=∠CAE？若存在，求出点P的横坐标；若不存在，请说明理由．
【答案】
（1）
解：把A、B两点坐标代入解析式可得 
，解得 
，
∴抛物线解析式为y= 
x2+ 
x﹣5
（2）
解：在y= x2+ x﹣5中，令x=0可得y=﹣5，
∴C（0，﹣5），
∵S△ABE=S△ABC，且E点在x轴下方，
∴E点纵坐标和C点纵坐标相同，
当y=﹣5时，代入可得 x2+ x=﹣5，解得x=﹣2或x=0（舍去），
∴E点坐标为（﹣2，﹣5）；
（3）
解：假设存在满足条件的P点，其坐标为（m， m2+ m﹣5），
如图，连接AP、CE、AE，过E作ED⊥AC于点D，过P作PQ⊥x轴于点Q，
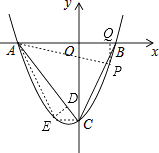
则AQ=AO+OQ=5+m，PQ=| m2+ m﹣5|，
在Rt△AOC中，OA=OC=5，则AC=5 
，∠ACO=∠DCE=45°，
由（2）可得EC=2，在Rt△EDC中，可得DE=DC= ，
∴AD=AC﹣DC=5 ﹣ =4 ，
当∠BAP=∠CAE时，则△EDA∽△PQA，
∴ 
= 
，即 
= 
，
∴ m2+ m﹣5= 
（5+m）或 m2+ m﹣5=﹣ （5+m），
当 m2+ m﹣5= （5+m）时，整理可得4m2﹣5m﹣75=0，解得m= 
或m=﹣5（与A点重合，舍去），
当 m2+ m﹣5=﹣ （5+m）时，整理可得4m2+11m﹣45=0，解得m= 
或m=﹣5（与A点重合，舍去），
∴存在满足条件的点P，其横坐标为 或
【解析】本题主要考查二次函数的综合运用．涉及到的知识点有待定系数法、三角形的面积、相似三角形的判定和性质及分类讨论等．在（3）中利用∠BAP=∠CAE构造三角形相似是解题的关键．本题考查知识点较多，综合性很强，难度适中．（1）把A、B两点的坐标代入，利用待定系数法可求得抛物线的解析式；（2）当S△ABE=S△ABC时，可知E点和C点的纵坐标相同，可求得E点坐标；（3）在△CAE中，过E作ED⊥AC于点D，可求得ED和AD的长度，设出点P坐标，过P作PQ⊥x轴于点Q，由条件可知△EDA∽△PQA，利用相似三角形的对应边可得到关于P点坐标的方程，可求得P点坐标．
【考点精析】解答此题的关键在于理解三角形的面积的相关知识，掌握三角形的面积=1/2×底×高，以及对相似三角形的判定与性质的理解，了解相似三角形的一切对应线段(对应高、对应中线、对应角平分线、外接圆半径、内切圆半径等）的比等于相似比；相似三角形周长的比等于相似比；相似三角形面积的比等于相似比的平方．
