题目内容
【题目】如图,四边形ABCD、CDEF、EFGH都是正方形.
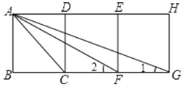
(1)求证:△ACF∽△GCA;
(2)求∠1+∠2的度数.
【答案】(1)证明参见解析;(2)45°.
【解析】
试题分析:(1)根据已知条件计算出相应的线段长度,可利用两边对应成比例,夹角相等判定两个三角形相似;(2)利用上题的相似得出对应角相等,即∠1=∠CAF,把∠1+∠2转换成∠CAF+∠2,即∠ACB,由正方形性质即可得出结论.
试题解析:(1)因为四边形ABCD、CDEF、EFGH都是正方形.所以可设边长为1,于是AC=![]() ,CF=1,AF=
,CF=1,AF=![]() ,CG=2,AG=
,CG=2,AG=![]() ,所以
,所以![]() ,又因为∠ACF是△ACF与△GCA的公共角,所以△ACF∽△GCA;(2)因为AC是正方形ABCD的对角线,所以∠ACB=45°,因为△ACF∽△GCA,所以∠1=∠CAF,又因为∠ACB是△ACF与△GCA的外角,所以∠1+∠2=∠CAF+∠2=∠ACB,所以∠1+∠2=45°.
,又因为∠ACF是△ACF与△GCA的公共角,所以△ACF∽△GCA;(2)因为AC是正方形ABCD的对角线,所以∠ACB=45°,因为△ACF∽△GCA,所以∠1=∠CAF,又因为∠ACB是△ACF与△GCA的外角,所以∠1+∠2=∠CAF+∠2=∠ACB,所以∠1+∠2=45°.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目