��Ŀ����
�������û������ܾ�ð���̡�.ij�й�����˾����̭ijһ����·�ϡ�ð���̡������صĹ��������ƻ�����A�ͺ�B�����ֻ������ܹ�������10��. ������A������1����B������2��������400��Ԫ��������A������2����B������1��������350��Ԫ.
(1) ����A�ͺ�B������ÿ�����������Ԫ��
(2) Ԥ���ڸ���·��A�ͺ�B������ÿ������ؿ����ֱ�Ϊ60���˴κ�100���˴�. ���ù�˾����A�ͺ�B���������ܷ��ò�����1200��Ԫ����ȷ����10���������ڸ���·������ؿ����ܺͲ�����680���˴Σ���ù�˾���ļ��ֹ������������ֹ����������ܷ������٣������ܷ����Ƕ��٣�
(1) ����A�ͺ�B������ÿ�����������Ԫ��
(2) Ԥ���ڸ���·��A�ͺ�B������ÿ������ؿ����ֱ�Ϊ60���˴κ�100���˴�. ���ù�˾����A�ͺ�B���������ܷ��ò�����1200��Ԫ����ȷ����10���������ڸ���·������ؿ����ܺͲ�����680���˴Σ���ù�˾���ļ��ֹ������������ֹ����������ܷ������٣������ܷ����Ƕ��٣�
��1������A�ͺ�B������ÿ������100��Ԫ��150��Ԫ
��2���ù�˾��3�ֹ�����������3�ֹ����������ܷ������٣������ܷ�����1100��Ԫ��
��2���ù�˾��3�ֹ�����������3�ֹ����������ܷ������٣������ܷ�����1100��Ԫ��
�����������1������֪�ɵó���Ԫһ�η����飬�������
��2����������ɵò���ʽ�飬�����Χ��Ҫע��ȡ�������ɵ÷����������ÿ�������ķ��ü��ɵ����ٷ���
�����������1���蹺��ÿ��A������x��Ԫ������ÿ��B������ÿ��y��Ԫ���������з��̵ã�
 �����
�����
��2���蹺��x��A������������10-x����B���������������в���ʽ��ã�

���

�����ַ�����һ������A������6����B������4��
����A������7����B������3��
����������A������8����B������2��
��A�������ϱ��ˣ��ʹ���A�ͳ��������ʱ���ܷ������٣��������ֹ�������
���ٷ���Ϊ��8��100+150��2=1100����Ԫ��
�𣺣�1������A�ͺ�B������ÿ������100��Ԫ��150��Ԫ
��2���ù�˾��3�ֹ�����������3�ֹ����������ܷ������٣������ܷ�����1100��Ԫ��

��ϰ��ϵ�д�
 �Ķ��쳵ϵ�д�
�Ķ��쳵ϵ�д�
�����Ŀ
 ������
������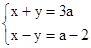 �Ľ�
�Ľ� �����
����� ��ȡֵ��Χ���������ϱ�ʾ����.
��ȡֵ��Χ���������ϱ�ʾ����. �У����ڵ�
�У����ڵ� �����ǰѵ�
�����ǰѵ� ������
������ �İ���㣬��֪��
�İ���㣬��֪�� �İ����Ϊ
�İ����Ϊ ����
���� ����
���� �������������εõ���
�������������εõ��� ����.����
����.���� ������Ϊ ������
������Ϊ ������ ��
�� �������������������
������������������� ����
���� ���Ϸ�����
���Ϸ����� ����֪����������û�3�κ�ȫ������ľ�飨ľ���㹻���ҵ�һ���û�����������ľ��ij�����a cm���������ܳ���Ϊ6cm����a��ȡֵ��Χ�� ��
����֪����������û�3�κ�ȫ������ľ�飨ľ���㹻���ҵ�һ���û�����������ľ��ij�����a cm���������ܳ���Ϊ6cm����a��ȡֵ��Χ�� ��