题目内容
已知关于x的一元二次方程x2-(m-1)x+m+2=0.
(1)若方程有两个相等的实数根,求m的值;
(2)若方程的两实数根之积等于m2-9m+2,求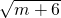 的值.
的值.
解:(1)∵方程有两个相等的实数根,
∴(m-1)2-4(m+2)=0,
∴m2-2m+1-4m-8=0,
m2-6m-7=0,
∴m=7或-1;
(2)∵方程的两实数根之积等于m2-9m+2,
∴m2-9m+2=m+2,
∴m2-10m=0,
∴m=0或m=10,
当m=0时,方程为:x2+x+2=0,方程没有实数根,舍去;
∴m=10,
∴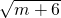 =4.
=4.
分析:(1)由于方程有两个相等的实数根,利用判别式可以列出关于m的方程即可求解;
(2)由于方程的两实数根之积等于m2-9m+2,利用根与系数即可得到关于m的方程,解方程即可求解.
点评:此题主要考查了一元二次方程的判别式与根与系数的关系的应用,同时考查了学生的综合应用能力及推理能力.
∴(m-1)2-4(m+2)=0,
∴m2-2m+1-4m-8=0,
m2-6m-7=0,
∴m=7或-1;
(2)∵方程的两实数根之积等于m2-9m+2,
∴m2-9m+2=m+2,
∴m2-10m=0,
∴m=0或m=10,
当m=0时,方程为:x2+x+2=0,方程没有实数根,舍去;
∴m=10,
∴
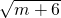 =4.
=4.分析:(1)由于方程有两个相等的实数根,利用判别式可以列出关于m的方程即可求解;
(2)由于方程的两实数根之积等于m2-9m+2,利用根与系数即可得到关于m的方程,解方程即可求解.
点评:此题主要考查了一元二次方程的判别式与根与系数的关系的应用,同时考查了学生的综合应用能力及推理能力.

练习册系列答案
 学习实践园地系列答案
学习实践园地系列答案
相关题目
已知关于x的一元二次x2-6x+k+1=0的两个实数根x1,x2,
+
=1,则k的值是( )
| 1 |
| x1 |
| 1 |
| x2 |
| A、8 | B、-7 | C、6 | D、5 |
 .
. .
.