题目内容
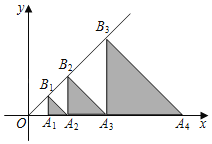
【题目】如图,在平面直角坐标系中,点A1,A2,A3…都在x轴上,点B1,B2,B3…都在直线y=x上,OA1=1,且△B1AA2,△B2A2A3,△B3A3A4,…△BnAnAn+1…分别是以A1,A2,A3,…An为直角顶点的等腰直角三角形,则△B2019A2019A2020的面积是( )
A.22018B.22019C.24035D.24036
【答案】C
【解析】
根据OA1=1,可得点A1的坐标为(1,0),然后根据△OA1B1,△B1A1A2,△B2B1A2,△B2A2A3,△B3B2A3…都是等腰直角三角形,求出A1A2,B1A2,A2A3,B2A3…的长度,然后找出规律,求出点B2019的坐标.结合等腰直角三角形的面积公式解答.
解:∵OA1=1,
∴点A1的坐标为(1,0),
∵△OA1B1是等腰直角三角形,
∴A1B1=1,
∴B1(1,1),
∵△B1A1A2是等腰直角三角形,
∴A1A2=1,B1A2=![]() ,
,
∵△B2B1A2为等腰直角三角形,
∴A2A3=2,
∴B2(2,2),
同理可得,B3(22,22),B4(23,23),…Bn(![]() ,
,![]() ),
),
∴点B2019的坐标是(22018,22018).
∴△B2019A2019A2020的面积=![]() .
.
故选:C.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目