题目内容
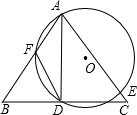 已知如图,在△ABC中,∠BAC=90°,AB=AC=
已知如图,在△ABC中,∠BAC=90°,AB=AC=| 2 |
| ||
| 2 |
分析:连接EF,DE,根据题意,可得EF为⊙O的直径,继而推出△EDC≌△FDA,AF=CE,然后在Rt△AEF中,根据勾股定理,即可求出AF的长度,由∠ADF=∠AEF,即可推出∠ADF的正弦值.
解答: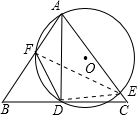 解:连接EF,ED(1分)
解:连接EF,ED(1分)
在△ABC中
∵AB=AC,∠BAC=90°,BD=CD,
∴AD=
BC=CD,∠DAF=∠DCE=45°,∠ADC=90°,(2分)
∴∠ADE+∠EDC=90°,
在⊙O中,
∵∠BAC=90°,
∴EF是⊙O的直径,(3分)
∴∠FDE=90°,
∴∠FDA+∠ADE=90°,
∴∠EDC=∠FDA,
∴△EDC≌△FDA,
∴AF=CE,(4分)
设AF=x,则CE=x,AE=AC-CE=
+1-x,
∵⊙O的半径是
,
∴EF=
,
在Rt△AEF中,x2+(
+1-x)2=(
)2,
解得x1=1,x2=
,
∠ADF=∠AEF,(5分)
∴当x=1时,sin∠ADF=sin∠AEF=
=
,
当x=
时,sin∠ADF=sin∠AEF=
=
,
∴∠ADF的正弦值为
或
.(7分)
 解:连接EF,ED(1分)
解:连接EF,ED(1分)在△ABC中
∵AB=AC,∠BAC=90°,BD=CD,
∴AD=
| 1 |
| 2 |
∴∠ADE+∠EDC=90°,
在⊙O中,
∵∠BAC=90°,
∴EF是⊙O的直径,(3分)
∴∠FDE=90°,
∴∠FDA+∠ADE=90°,
∴∠EDC=∠FDA,
∴△EDC≌△FDA,
∴AF=CE,(4分)
设AF=x,则CE=x,AE=AC-CE=
| 2 |
∵⊙O的半径是
| ||
| 2 |
∴EF=
| 3 |
在Rt△AEF中,x2+(
| 2 |
| 3 |
解得x1=1,x2=
| 2 |
∠ADF=∠AEF,(5分)
∴当x=1时,sin∠ADF=sin∠AEF=
| AF |
| EF |
| ||
| 3 |
当x=
| 2 |
| AF |
| EF |
| ||
| 3 |
∴∠ADF的正弦值为
| ||
| 3 |
| ||
| 3 |
点评:本题主要考查了圆周角定理、全等三角形的判定和性质、解直角三角形、勾股定理等知识点,解题的关键在于求出AF=CE,解Rt△AEF,∠ADF=∠AEF.

练习册系列答案
相关题目
 18、已知如图:在△ABC中,AB=AC,D在BC上,且DE∥AC交AB于E,点F在AC上,且DF=DC.求证:
18、已知如图:在△ABC中,AB=AC,D在BC上,且DE∥AC交AB于E,点F在AC上,且DF=DC.求证: (2012•通州区一模)已知如图,在△ABC中,AB=AC,∠ABC=α,将△ABC以点B为中心,沿逆时针方向旋转α度(0°<α<90°),得到△BDE,点B、A、E恰好在同一条直线上,连接CE.
(2012•通州区一模)已知如图,在△ABC中,AB=AC,∠ABC=α,将△ABC以点B为中心,沿逆时针方向旋转α度(0°<α<90°),得到△BDE,点B、A、E恰好在同一条直线上,连接CE. 已知如图,在△ABC中,∠B=30°,∠C=45°,AB-AC=2-
已知如图,在△ABC中,∠B=30°,∠C=45°,AB-AC=2- 已知如图,在△ABC中,∠C=60°,AB=
已知如图,在△ABC中,∠C=60°,AB= 已知如图,在△ABC中,AD平分∠BAC交BC于D,E为AD延长线上一点且∠ACE=∠B.求证:CD=CE.
已知如图,在△ABC中,AD平分∠BAC交BC于D,E为AD延长线上一点且∠ACE=∠B.求证:CD=CE.