Question

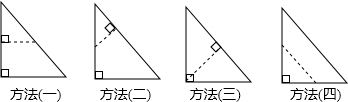
（1）如图，有四个直角三角形，在提供的三角形中，只有一刀剪下一个与原三角形相似的三角形，请在图上画出四种不同的裁剪方法（标出必要的记号）；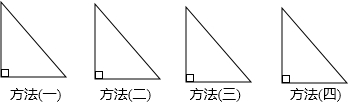
．
（2）根据（1）的某种剪法，作为解决下列问题的突破口，先按裁剪法构图（作辅助线），后解决问题．
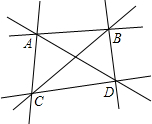
问题：在四边形ABCD中，AB=2，CD=1，∠A=60°，∠B=∠D=90°，求BC和AD．
．

Answer 1

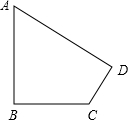分析：（1）如图，分别作直角边或斜边的垂线，作斜边的平行线，可得到与原三角形相似的三角形；
（2）分别作DE⊥AB，CF⊥DE，垂足为E、F，将原四边形剪切为两个30°的直角三角形和一个矩形，再解直角三角形．

解答：解：（1）如图，作垂线或平行线；


（2）如图，作DE⊥AB，CF⊥DE，垂足为E、F，
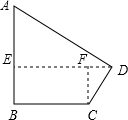
∵∠A=60°，∠B=∠D=90°，
∴∠BCD=360°-∠A-∠B-∠D=′120°，
在Rt△CDF中，CD=1，∠DCF=∠BCD-∠BCF=30°，
DF=CD•sin30°=

1

2

，CF=CD•cos30°=

3

2

；
∴BE=CF=

3

2

，AE=AB-BE=2-

3

2

；
在Rt△ADE中，∠ADE=90°-∠CDF=30°，
∴DE=

AE

tan30°

=2

3

-

3

2

，
BC=EF=DE-DF=2

3

-2，
AD=

AE

sin30°

=4-

3

．

点评：图形相似的作图方法，割补法解决不规则图象的有关计算问题，体现了转化的数学思想．