题目内容
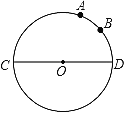
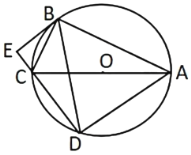
【题目】如图,![]() 为
为![]() 的直径,点
的直径,点![]() 、
、![]() 是
是![]() 上两点,
上两点,![]() ,
,![]() 交
交![]() 的延长线于点
的延长线于点![]() .
.
(1)求证:![]() .
.
(2)若![]() ,
,![]() 的半径为5,求
的半径为5,求![]() 的值.
的值.
【答案】(1)证明见详解;(2)![]() .
.
【解析】
(1)连结OB和OD,证出OB∥DE,根据平行线的性质可以得到∠ECB=∠OBC,根据等腰三角形的性质可得∠OBC=∠BCA,从而得出![]() ;
;
(2)作CH⊥OB于H,解直角三角形求出BE,BC,再证明∠BDC=∠EBC,可得sin∠BDC=sin∠EBC=![]() ,即可解决问题.
,即可解决问题.

解:(1)连结OB和OD,
在△BOD和△BOA中,
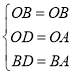
∴△BOD≌△BOA(SSS)
∴∠BDO=∠BAO
∵∠BDO=∠OBD,∠BAO=∠BDC
∴∠BDC=∠OBD
∴OB∥DE
∴∠ECB=∠OBC
∵∠OBC=∠BCA
∴∠ECB=∠BCA
(2)作CH⊥OB于H
由(1)知OB∥DE
∴∠HBE=∠E=90°
∵∠CHB=∠HBE=∠E=90°
∴四边形BECH是矩形
∴BH=CE=2
∵OA=OB=OC=5
∴OH=3,CH=BE=![]() =4
=4
∴BC=![]()
∵∠EBC+∠OBC=90°,∠OBC+∠OBA=90°
∴∠EBC=∠OBC
∵∠BDC=∠BAO=∠OBA
∴∠BDC=∠EBC
∴sin∠BDC=sin∠EBC=![]()
![]()
故答案为![]() .
.

练习册系列答案
相关题目