题目内容
【题目】在平面直角坐标系![]() 中,对于点
中,对于点![]() 和
和![]() ,给出如下定义:若
,给出如下定义:若![]() 上存在一点
上存在一点![]() 不与
不与![]() 重合,使点
重合,使点![]() 关于直线
关于直线![]() 的对称点
的对称点![]() 在
在![]() 上,则称
上,则称![]() 为
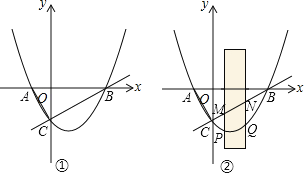
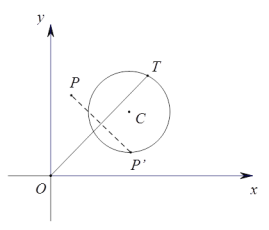
为![]() 的反射点.下图为
的反射点.下图为![]() 的反射点
的反射点![]() 的示意图.
的示意图.
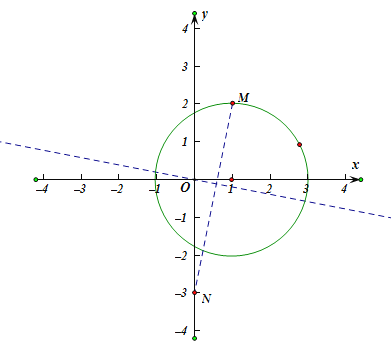
(1)已知点![]() 的坐标为
的坐标为![]() ,
,![]() 的半径为
的半径为![]() ,
,
①在点![]() ,
,![]() ,
,![]() 中,
中,![]() 的反射点是____________;
的反射点是____________;
②点![]() 在直线
在直线![]() 上,若
上,若![]() 为
为![]() 的反射点,求点
的反射点,求点![]() 的横坐标的取值范围;
的横坐标的取值范围;
(2)![]() 的圆心在
的圆心在![]() 轴上,半径为
轴上,半径为![]() ,
,![]() 轴上存在点
轴上存在点![]() 是
是![]() 的反射点,直接写出圆心
的反射点,直接写出圆心![]() 的横坐标
的横坐标![]() 的取值范围.
的取值范围.
【答案】(1)①![]() ,
,![]() ;②点
;②点![]() 的横坐标
的横坐标![]() 的取值范围是
的取值范围是![]() ,或
,或![]() ;(2)圆心
;(2)圆心![]() 的横坐标
的横坐标![]() 的取值范围是
的取值范围是![]() .
.
【解析】
(1)①连接MN,过原点O作MN的垂线,必与![]() 有交点,即可得出结论.
有交点,即可得出结论.
②直线![]() 与以原点为圆心,半径为1和3的两个圆的交点从左至右依次为
与以原点为圆心,半径为1和3的两个圆的交点从左至右依次为![]() ,
,![]() ,
,![]() ,
,![]() ,过点
,过点![]() 作
作![]() 轴于点
轴于点![]() ,分别求出点E,F,G,H的坐标,
,分别求出点E,F,G,H的坐标,![]() 为
为![]() 的反射点,则
的反射点,则![]()
上存在一点T,使点P关于直线OT的对称点![]() 在
在![]() 上,则
上,则![]() ,由
,由![]() ,则
,则![]() ,即可求出答案.
,即可求出答案.
(2)根据反射点的定义求解即可.
解(1)①连接MN,过原点O作MN的垂线,必与![]() 有交点,
有交点, ![]() 都是
都是![]() 的反射点.
的反射点.
②设直线![]() 与以原点为圆心,半径为1和3的两个圆的交点从左至右依次为
与以原点为圆心,半径为1和3的两个圆的交点从左至右依次为![]() ,
,![]() ,
,![]() ,
,![]() ,过点
,过点![]() 作
作![]() 轴于点
轴于点![]() ,如图.
,如图.
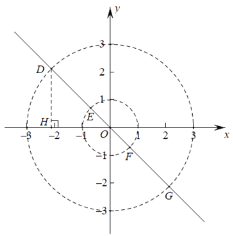
可求得点![]() 的横坐标为
的横坐标为![]() .
.
同理可求得点![]() ,
,![]() ,
,![]() 的横坐标分别为
的横坐标分别为![]() ,
,![]() ,
,![]() .
.
点![]() 是
是![]() 的反射点,则
的反射点,则![]() 上存在一点
上存在一点![]() ,使点
,使点![]() 关于直线
关于直线![]() 的对称点
的对称点![]() 在
在![]() 上,则
上,则![]() .
.
∵![]() ,∴
,∴![]() .
.
反之,若![]() ,
,![]() 上存在点
上存在点![]() ,使得
,使得![]() ,故线段
,故线段![]() 的垂直平分线经过原点,且与
的垂直平分线经过原点,且与![]() 相交.因此点
相交.因此点![]() 是
是![]() 的反射点.
的反射点.
∴点![]() 的横坐标
的横坐标![]() 的取值范围是
的取值范围是![]() ,或
,或![]() .
.
(2)圆心![]() 的横坐标
的横坐标![]() 的取值范围是
的取值范围是![]() .
.

练习册系列答案
相关题目