题目内容
在平面直角坐标系xOy中,二次函数 的图象经过(
的图象经过( ,0)和(
,0)和( ,0)两点.
,0)两点.
(1)求此二次函数的表达式.
(2)直接写出当 <x<1时,y的取值范围.
<x<1时,y的取值范围.
(3)将一次函数 y=(1-m)x+2的图象向下平移m个单位后,与二次函数 图象交点的横坐标分别是a和b,其中a<2<b,试求m的取值范围.
图象交点的横坐标分别是a和b,其中a<2<b,试求m的取值范围.
(1) ;(2)
;(2) <y<3;(3)m<
<y<3;(3)m<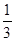 的全体实数.
的全体实数.
解析试题分析:(1)根据点在曲线上点的坐标满足方程的关系,由二次函数 的图象经过(
的图象经过( ,0)和(
,0)和( ,0)两点,列方程组求解即可.
,0)两点,列方程组求解即可.
(2)作图观察即可;
(3)根据题意,得到平移后的一次函数表达式,由a<2<b得 ,取x=2,解出即可.
,取x=2,解出即可.
试题解析:(1)由二次函数的图象经过( ,0)和(
,0)和( ,0)两点,得
,0)两点,得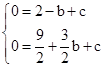 解这个方程组,得
解这个方程组,得
∴此二次函数的表达式为 .
.
(2)如图,当x= 时,y=3,当x=1时y=
时,y=3,当x=1时y=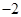 ,
,
又二次函数的顶点坐标是( ).
).
∴当 <x<1时y的取值范围是
<x<1时y的取值范围是 <y<3.
<y<3.
(3)将一次函数  的图象向下平移m个单位后的一次函数表达式为
的图象向下平移m个单位后的一次函数表达式为 .
.
∵ 与二次函数
与二次函数 图象交点的横坐标为a和b,
图象交点的横坐标为a和b,
∴ ,整理得
,整理得 .
.
∵a<2<b,∴a≠b.∴ ,
,
∴m≠1.
∵a和b满足a<2<b,∴如图,当x=2时, .
.
把x=2代入 ,解得m<
,解得m<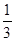 ,
,
∴m的取值范围为m<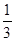 的全体实数.
的全体实数.
考点:1.二次函数综合题;2.平移问题;3.待定系数法的应用;4.曲线上点的坐标与方程的关系;5.二次函数与不等式和方程的关系;6.数形结合思想的应用.

练习册系列答案
 快乐小博士巩固与提高系列答案
快乐小博士巩固与提高系列答案
相关题目
某商品现在的售价为每件35元.每天可卖出50件.市场调查反映:如果调整价格.每降价1元,每天可多卖出2件.请你帮助分析,当每件商品降价多少元时,可使每天的销售额最大,最大销售额是多少?
设每件商品降价x元.每天的销售额为y元.
(1)分析:根据问题中的数量关系.用含x的式子填表:
| | 原价 | 每件降价1元 | 每件降价2元 | … | 每件降价x元 |
| 每件售价(元) | 35 | 34 | 33 | … | |
| 每天售量(件) | 50 | 52 | 54 | … | |
(2)(由以上分析,用含x的式子表示y,并求出问题的解)
 =
= ,求k;
,求k;
 x2+bx+c经过点B,且顶点在直线x=
x2+bx+c经过点B,且顶点在直线x= 上.
上.
 中,矩形
中,矩形 的边
的边 在
在 轴上,且
轴上,且 ,
, ,直线
,直线 经过点
经过点 ,交
,交 轴于点
轴于点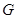 .
. 的坐标分别是
的坐标分别是 的抛物线的解析式;
的抛物线的解析式; ,顶点为点
,顶点为点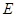 .求出当
.求出当 时抛物线的解析式.
时抛物线的解析式.
 的方程:
的方程: ①和
①和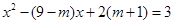 ②,其中
②,其中 .
. 的图象与
的图象与 、
、 两点(点
两点(点 处,点
处,点 处,若点
处,若点 的值;
的值; ,在(2)的条件下,函数
,在(2)的条件下,函数 ,
, 的图象位于直线
的图象位于直线 左侧的部分与直线
左侧的部分与直线 (
( )交于两点,当向上平移直线
)交于两点,当向上平移直线 的值是________________.
的值是________________.
 与
与 轴交于
轴交于 两点,与
两点,与 轴交于点
轴交于点 ,连结AC,若
,连结AC,若
 时,求出点
时,求出点 的坐标;
的坐标; ,
, 是线段
是线段 、
、 重合)的一个动点.过点
重合)的一个动点.过点 ,交抛物线于点
,交抛物线于点 ,连结
,连结 、
、 ,设点
,设点 的面积最大?最大面积为多少?
的面积最大?最大面积为多少?
 ,抛物线y = ax2+bx+2经过点A(m,0),B(2,0),D
,抛物线y = ax2+bx+2经过点A(m,0),B(2,0),D  三点.
三点.
 ,
, 求该抛物线与x轴的交点坐标;
求该抛物线与x轴的交点坐标; ,证明抛物线与x轴有两个交点;
,证明抛物线与x轴有两个交点; 且抛物线在
且抛物线在 区间上的最小值是-3,求b的值.
区间上的最小值是-3,求b的值.