题目内容
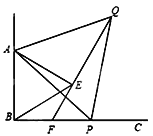
【题目】如图,已知△ABC和△ADE均为等边三角形,D在BC上,DE与AC相交于点F,BD=3,CF=2,则△ADE的周长=________.
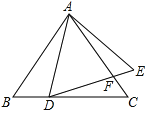
【答案】![]()
【解析】
利用两对相似三角形,线段成比例:AB:BD=AE:EF,AB:AD=AE:AF,可得AD2=AB×AF ,又同理可得CD:CF=AE:EF,可得AB:BD=CD:CF,进而得出AB和AF,即可得出AD,即可得解.
∵△ABC和△ADE均为等边三角形,
∴∠B=∠BAC=60°,∠E=∠EAD=60°,
∴∠B=∠E,∠BAD=∠EAF,
∴△ABD∽△AEF,
∴AB:BD=AE:EF,AB:AD=AE:AF,
∴AD2=AB×AF
同理:△CDF∽△EAF,
∴CD:CF=AE:EF,
∴AB:BD=CD:CF,
∵BD=3,CF=2,CD=AB-BD
∴AB:3=(AB-3):2
∴AB=9
∴AF=9-2=7
∴AD=![]()
∴△ADE的周长为![]() .
.

练习册系列答案
相关题目