Question

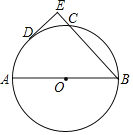
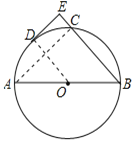
【题目】如图，AB是⊙O的直径，点C、D在半圆上，，过D作DE⊥BC于E．

（1）求证：DE是⊙O的切线.

（2）若DE＝2CE＝4，求⊙O的半径．

Answer 1

【答案】（1）证明见解析；（2）5

【解析】

（1）如图，连接OD、AC，由AB是直径可得∠ACB=90°，根据DE⊥BC可得DE//AC，根据垂径定理的推论可得OD⊥AC，即可证明OD⊥DE，由点D在圆上即可证明DE是⊙O的切线；（2）作OF⊥BC于F，可得四边形OFED是矩形，可得OF＝DE＝4，OD＝EF，由垂径定理可得BF＝CF，设⊙O的半径为R，在Rt△AOF中，利用勾股定理求出R值即可.

（1）如图，连接OD、AC，

∵AB是⊙O的直径，

∴∠ACB＝90°，

∴AC⊥BC，

∵DE⊥BC，

∴DE∥AC，

∵，

∴OD⊥AC，

∴DE⊥OD，

∵D在⊙O上，

∴DE是⊙O的切线；

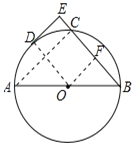
（2）如图，作OF⊥BC于F，

∴BF＝CF，

∵DE⊥BE，OD⊥DE，OF⊥BC，

∴四边形OFED是矩形，

∴OF＝DE＝4，OD＝EF，

∵DE＝2CE＝4，

∴CE＝2，

设⊙O的半径为R，则BF＝CF＝R﹣2，

在Rt△BOF中，BF2+OF2＝OA2，

∴（R﹣2）2+42＝R2，

解得R＝5，

即⊙O的半径为5．