��Ŀ����
����Ŀ����ͼ��ֱ��y=2x+2��x�ύ�ڵ�A����y�ύ�ڵ�B���ѡ�AOB��y�ᷭ�ۣ���A�䵽��C������B��������y=-x2+bx+c��ֱ��BC���ڵ�D��3��-4����
��1����ֱ��BD�������ߵĽ���ʽ��
��2���ڵ�һ�����ڵ��������ϣ��Ƿ����һ��M����MN��ֱ��x�ᣬ����Ϊ��N��ʹ����M��O��NΪ��������������BOC���ƣ������ڣ������M�����ꣻ�������ڣ���˵�����ɣ�
��3����ֱ��BD�Ϸ�������������һ����P������P��PH��ֱ��x�ᣬ��ֱ��BD�ڵ�H�����ı���BOHP��ƽ���ı���ʱ������P�����꣮
���𰸡���1��ֱ��BD�Ľ���ʽΪ��y=-2x+2��y=-x2+x+2����2����1��2������![]() ��
��![]() ������3��P���������1��2����2��0����
������3��P���������1��2����2��0����
��������
�����������1����ֱ��y=2x+2�������A��B�����꣬�ɴ���ϵ�����Ϳ�����������ߵĽ���ʽ��ֱ��BD�Ľ���ʽ��
��2����ͼ1��2���ɣ�1���Ľ���ʽ��M��a��-a2+a+2��������BOC�ס�MON���BOC�ס�ONMʱ�������������ε����ʾͿ���������ۣ�
��3����P��b��-b2+b+2����H��b��-2b+2������ƽ���ı��ε����ʽ����������b��ֵ�Ϳ���������ۣ�
�����������1����y=2x+2��
�൱x=0ʱ��y=2��
��B��0��2����
��y=0ʱ��x=-1��
��A��-1��0����
��������y=-x2+bx+c����B��0��2����D��3��-4����
��![]()
��ã�![]() ��
��
��y=-x2+x+2��
��ֱ��BD�Ľ���ʽΪy=kx+b�������⣬��
![]() ��
��
��ã�![]() ��
��
��ֱ��BD�Ľ���ʽΪ��y=-2x+2��
��2�����ڣ�
��ͼ1��
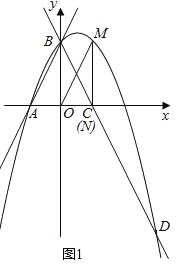
��M��a��-a2+a+2����
��MN��ֱ��x�ᣬ
��MN=-a2+a+2��ON=a��
��y=-2x+2��
��y=0ʱ��x=1��
��C��1��0����
��OC=1��
��B��0��2����
��OB=2��
����BOC�ס�MNOʱ��
��![]() ��
��
��![]() ��
��
��ã�a1=1��a2=-2����ȥ��
��M��1��2����
��ͼ2��
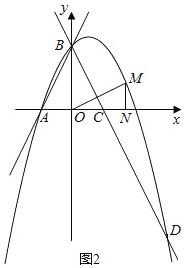
����BOC�ס�ONMʱ��
![]() ��
��
��![]() ��
��
��a=![]() ��
��![]() ����ȥ����
����ȥ����
��M��![]() ��
��![]() ����
����
����������ĵ�M������Ϊ��1��2������![]() ��
��![]() ����
����
��3����P��b��-b2+b+2����H��b��-2b+2����
��ͼ3��
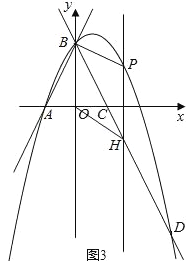
���ı���BOHP��ƽ���ı��Σ�
��BO=PH=2��
��PH=-b2+b+2+2b-2=-b2+3b��
��2=-b2+3b
��b1=1��b2=2��
��b=1ʱ��P��1��2����
��b=2ʱ��P��2��0��
��P���������1��2����2��0����

 ��ս100��Ԫ����Ծ�ϵ�д�
��ս100��Ԫ����Ծ�ϵ�д�