题目内容
设a、b、c为实数，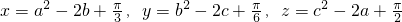
，则x、y、z中，至少有一个值
- A.大于0
- B.等于0
- C.不大于0
- D.小于0
A
分析：首先由x+y+z得出={（a-1）2}+{（b-1）2}+{（c-1）2}+π-3，根据偶次方的非负性，得出x、y、z中至少有一个大于0．
解答：因x+y+z={（a-1）2}+{（b-1）2}+{（c-1）2}+π-3＞0，
则x、y、z中至少有一个大于0，
故选：A．
点评：此题考查的知识点是完全平方公式，关键是把x、y、z相加，运用完全平方公式得出x+y+z={（a-1）2}+{（b-1）2}+{（c-1）2}+π-3＞0．
分析：首先由x+y+z得出={（a-1）2}+{（b-1）2}+{（c-1）2}+π-3，根据偶次方的非负性，得出x、y、z中至少有一个大于0．
解答：因x+y+z={（a-1）2}+{（b-1）2}+{（c-1）2}+π-3＞0，
则x、y、z中至少有一个大于0，
故选：A．
点评：此题考查的知识点是完全平方公式，关键是把x、y、z相加，运用完全平方公式得出x+y+z={（a-1）2}+{（b-1）2}+{（c-1）2}+π-3＞0．
练习册系列答案
相关题目