题目内容
已知:如图,在△ABC中,D为A月边上一点,∠A=36°,AC=BC,AC2=AB?AD.
(1)试说明:△ADC和△BDC都是等腰三角形,
(2)若AB=1,求AC的长,
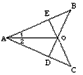
(3)试构造一个等腰梯形,要求该梯形连同它的两条对角线所形成的8个三角形中有尽可能多的等腰三角形.

解:(1)在△ABC中,AC=BC,∠A=36°,∴∠B=∠A=36°,∠ACB=108°
在△ABC与△CAD中,∠A=∠B=36°.
∵AC2=AB?AD,∴![]() .
.
∴△ABC∽△CAD.
∴∠ACD=∠B=36°.
∴∠CDB=72°,∠DCB=108°-36°=72°.
∴△ADC和△BDC都是等腰三角形.
(2)设AC=x,则AD=1-BD=1-BC=1-2x
∴x2=1×(1-x),即x2+x-1=0.解得![]() (舍去).
(舍去).
∴![]()
(3)说明:按照画出的梯形中,有4个,6个和8个等腰三角形三种情况分类得分.
①有4个等腰三角形,得1分;
②有6个等腰三角形,得2分;
③有8个等腰三角形,得4分.

练习册系列答案
 小学夺冠AB卷系列答案
小学夺冠AB卷系列答案 ABC考王全优卷系列答案
ABC考王全优卷系列答案
相关题目
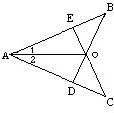 34、已知:如图,在AB、AC上各取一点,E、D,使AE=AD,连接BD,CE,BD与CE交于O,连接AO,∠1=∠2,
34、已知:如图,在AB、AC上各取一点,E、D,使AE=AD,连接BD,CE,BD与CE交于O,连接AO,∠1=∠2,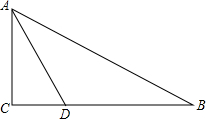 (2013•启东市一模)已知,如图,在Rt△ABC中,∠C=90°,∠BAC的角平分线AD交BC边于D.
(2013•启东市一模)已知,如图,在Rt△ABC中,∠C=90°,∠BAC的角平分线AD交BC边于D. 已知:如图,在△ABC中,∠C=120°,边AC的垂直平分线DE与AC、AB分别交于点D和点E.
已知:如图,在△ABC中,∠C=120°,边AC的垂直平分线DE与AC、AB分别交于点D和点E.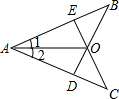 已知:如图,在AB、AC上各取一点E、D,使AE=AD,连接BD,CE,BD与CE交于O,连接AO,∠1=∠2,
已知:如图,在AB、AC上各取一点E、D,使AE=AD,连接BD,CE,BD与CE交于O,连接AO,∠1=∠2,