题目内容
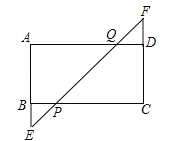
【题目】如图,矩形ABCD中,延长AB至E,延长CD至F,BE=DF,连接EF,与BC、AD分别相交于P、Q两点.
(1)求证:CP=AQ;
(2)若BP=1,PQ=![]() ,∠AEF=45°,求矩形ABCD的面积.
,∠AEF=45°,求矩形ABCD的面积.
【答案】(1)证明见解析;(2)8.
【解析】
试题分析:(1)由矩形的性质得出∠A=∠ABC=∠C=∠ADC=90°,AB=CD,AD=BC,AB∥CD,AD∥BC,证出∠E=∠F,AE=CF,由ASA证明△CFP≌△AEQ,即可得出结论;
(2)证明△BEP、△AEQ是等腰直角三角形,得出BE=BP=1,AQ=AE,求出PE=![]() BP=
BP=![]() ,得出EQ=PE+PQ=
,得出EQ=PE+PQ=![]() ,由等腰直角三角形的性质和勾股定理得出AQ=AE=3,求出AB=AE﹣BE=2,DQ=BP=1,得出AD=AQ+DQ=4,即可求出矩形ABCD的面积.
,由等腰直角三角形的性质和勾股定理得出AQ=AE=3,求出AB=AE﹣BE=2,DQ=BP=1,得出AD=AQ+DQ=4,即可求出矩形ABCD的面积.
试题解析:(1)证明:∵四边形ABCD是矩形,∴∠A=∠ABC=∠C=∠ADC=90°,AB=CD,AD=BC,AB∥CD,AD∥BC,∴∠E=∠F,∵BE=DF,∴AE=CF,在△CFP和△AEQ中,∵∠C=∠A,CF=AE,∠F=∠E,∴△CFP≌△AEQ(ASA),∴CP=AQ;
(2)解:∵AD∥BC,∴∠PBE=∠A=90°,∵∠AEF=45°,∴△BEP、△AEQ是等腰直角三角形,∴BE=BP=1,AQ=AE,∴PE=![]() BP=
BP=![]() ,∴EQ=PE+PQ=
,∴EQ=PE+PQ=![]() =
=![]() ,∴AQ=AE=3,∴AB=AE﹣BE=2,∵CP=AQ,AD=BC,∴DQ=BP=1,∴AD=AQ+DQ=3+1=4,∴矩形ABCD的面积=ABAD=2×4=8.
,∴AQ=AE=3,∴AB=AE﹣BE=2,∵CP=AQ,AD=BC,∴DQ=BP=1,∴AD=AQ+DQ=3+1=4,∴矩形ABCD的面积=ABAD=2×4=8.

 新活力总动员暑系列答案
新活力总动员暑系列答案 龙人图书快乐假期暑假作业郑州大学出版社系列答案
龙人图书快乐假期暑假作业郑州大学出版社系列答案【题目】九(1)班同学为了解2011年某小区家庭月均用水情况,随机调查了该小区部分家庭,并将调查数据进行如下整理.请解答以下问题:
(1)把下面的频数分布表和频数分布直方图补充完整;
月均用水量x(t) | 频数(户) | 频率 |
0<x≤5 | 6 | 0.12 |
5<x≤10 | 0.24 | |
10<x≤15 | 16 | 0.32 |
15<x≤20 | 10 | 0.20 |
20<x≤25 | 4 | |
25<x≤30 | 2 | 0.04 |
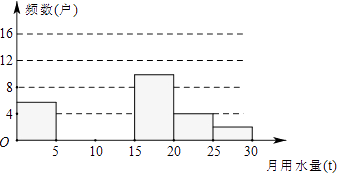
(2)求该小区用水量不超过15t的家庭占被调查家庭总数的百分比;
(3)若该小区有1000户家庭,根据调查数据估计,该小区月均用水量超过20t的家庭大约有多少户?