题目内容
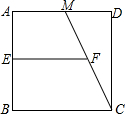如图，M是边长为2cm的正方形ABCD的边AD的中点，E、F分别是AB、CM的中点．则EF=分析：此题只需根据梯形的中位线定理进行求解．
解答：解：∵M是边长为2cm的正方形ABCD的边AD的中点，
∴AM=MD=1cm．
又∵E、F分别是AB、CM的中点，
∴EF=
（AM+BC）=
（1+2）=
=1.5（cm）．
∴AM=MD=1cm．
又∵E、F分别是AB、CM的中点，
∴EF=
| 1 |
| 2 |
| 1 |
| 2 |
| 3 |
| 2 |
点评：本题比较简单，考查的是正方形的性质和梯形的中位线定理．
练习册系列答案
相关题目
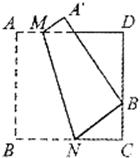20、如图，四边形ABCD是边长为9的正方形纸片，将其沿MN折叠，使点B落在CD边上的B′处，点A对应点为A′，且B′C=3，则AM的长是（ ）
如图，圆柱的轴截面ABCD是边长为4的正方形，动点P从A点出发，沿着圆柱的侧面移动到BC的中点S的最短距离为（ ）A、2
| ||
B、2
| ||
C、4
| ||
D、2
|
21、如图，方格纸上的每个小方格都是边长为1的正方形，我们把以格点间连线为边的三角形称为“格点三角形”，图中的△ABC就是格点三角形．在建立平面直角坐标系后，点B的坐标为（-2，-1）．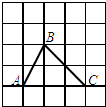
（2012•天桥区三模）在如图所示的5×5方格中，每个小方格都是边长为1的正方形，△ABC是格点三角形（即顶点恰好是正方形的顶点），则与△ABC有一条公共边且全等的所有格点三角形的个数是（ ）
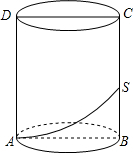如图，圆柱形玻璃器皿的轴截面ABCD是边长为4的正方形，一只蜘蛛在容器内底部的A点，一只苍蝇停在容器内BC的中点S处，蜘蛛若想吃到苍蝇，则它移动的最短距离是（ ）