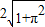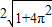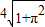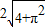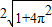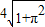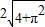题目内容
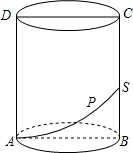
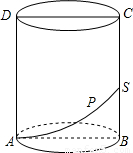
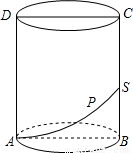
 如图,圆柱的轴截面ABCD是边长为4的正方形,动点P从A点出发,沿着圆柱的侧面移动到BC的中点S的最短距离为( )
如图,圆柱的轴截面ABCD是边长为4的正方形,动点P从A点出发,沿着圆柱的侧面移动到BC的中点S的最短距离为( )A、2
| ||
B、2
| ||
C、4
| ||
D、2
|
分析:要求动点P从A点出发,沿着圆柱的侧面移动到BC的中点S的最短距离,就要先把侧面积展开,得到一个矩形,然后再利用两点间线段最短,线段的距离.
解答:解:展开后矩形的长为
×π×4=2π,高为2,
所以利用勾股定理可得最短距离为
,
即2
.
故选A.
| 1 |
| 2 |
所以利用勾股定理可得最短距离为
| 4+4π2 |
即2
| 1+π2 |
故选A.
点评:本题的关键是明确,要求最短距离,就要先展开圆柱的侧面积,而且要注意展开后的矩形的长为周长的一半,而不是周长.

练习册系列答案
相关题目