题目内容
(2012•梁子湖区模拟)2011年上半年,黄冈大别山地区某市某种农产品受不良炒作的影响,价格一路上扬,8月初国家实施调控措施后,该农产品的价格开始回落,经市场调研发现,1月份至12月份,该农产品的月平均价格y(元/千克)与月份x之间的函数关系式对应的点都在如图所示的图象上;该图象从左至右,依次是线段AB、曲线BC,其中曲线BC为抛物线的一部分, 已知1月、7月、9月和12月这四个月的月平均价格分别为8元/千克、26元/千克、14元/千克、11元/千克.
已知1月、7月、9月和12月这四个月的月平均价格分别为8元/千克、26元/千克、14元/千克、11元/千克.
(1)求该农产品的月平均价格y(元/千克)与月份x之间的函数关系式?
(2)2011年的12个月中,这种农产品的月平均价格哪个月最低?最低为多少?
(3)若以12个月份的月平均价格的平均数为年平均价格,月平均价格高于年平均价格的月份有哪些?
 已知1月、7月、9月和12月这四个月的月平均价格分别为8元/千克、26元/千克、14元/千克、11元/千克.
已知1月、7月、9月和12月这四个月的月平均价格分别为8元/千克、26元/千克、14元/千克、11元/千克.(1)求该农产品的月平均价格y(元/千克)与月份x之间的函数关系式?
(2)2011年的12个月中,这种农产品的月平均价格哪个月最低?最低为多少?
(3)若以12个月份的月平均价格的平均数为年平均价格,月平均价格高于年平均价格的月份有哪些?
分析:(1)根据函数图象,函数解析式分为两段,当1≤x≤7时,为一次函数解析式,当7≤x≤12时,为二次函数解析式,分别设一次函数、二次函数解析式,根据图象上的点,分别求解析式;
(2)由图象可知一次函数最小值为8,用配方法求二次函数的顶点式,得出二次函数的最小值,比较最小值即可;
(3)由一次函数可知,以x=4时的月平均价格17代表前7个月的平均值,再根据二次函数解析式,分别求出后5个月的月的平均值,再求年平均价格,把那个月的月平均价格与年平均价格进行比较即可.
(2)由图象可知一次函数最小值为8,用配方法求二次函数的顶点式,得出二次函数的最小值,比较最小值即可;
(3)由一次函数可知,以x=4时的月平均价格17代表前7个月的平均值,再根据二次函数解析式,分别求出后5个月的月的平均值,再求年平均价格,把那个月的月平均价格与年平均价格进行比较即可.
解答:解:(1)当1≤x≤7时,设y=kx+m.
将点(1,8)、(7,26)分别代入y=kx+m,
得
解之,得
∴函数解析式为y=3x+5;
当7≤x≤12时,设y=ax2+bx+c(a≠0).
将(7,26)、(9,14)、(12,11)分别代入y=ax2+bx+c,
得:
解之,得
∴函数解析式为y=x2-22x+131.
故该农产品的月平均价格y(元/千克)与月份x之间的函数关系式为:
y=
;
(2)当1≤x≤7时,函数y=3x+5中y随x的增大而增大,
∴当x最小值=1时,y最小值=3×1+5=8.
当7≤x≤12时,y=x2-22x+131=(x-11)2+10,
∴当x=11时,y最小值=10.
所以,该农产品平均价格最低的是1月,最低为8元/千克.
(3)∵1至7月份的月平均价格呈一次函数,
∴x=4时的月平均价格17是前7个月的平均值.
将x=8,x=10和x=11分别代入y=x2-22x+131,得y=19,y=11和y=10.
∴后5个月的月平均价格分别为19,14,11,10,11.
∴年平均价格为
=
=
≈15.3(元/千克).
当x=3时,y=14<15.3.
∴4,5,6,7,8这五个月的月平均价格高于年平均价格.
将点(1,8)、(7,26)分别代入y=kx+m,
得
|
解之,得
|
∴函数解析式为y=3x+5;
当7≤x≤12时,设y=ax2+bx+c(a≠0).
将(7,26)、(9,14)、(12,11)分别代入y=ax2+bx+c,
得:
|
解之,得
|
∴函数解析式为y=x2-22x+131.
故该农产品的月平均价格y(元/千克)与月份x之间的函数关系式为:
y=
|
(2)当1≤x≤7时,函数y=3x+5中y随x的增大而增大,
∴当x最小值=1时,y最小值=3×1+5=8.
当7≤x≤12时,y=x2-22x+131=(x-11)2+10,
∴当x=11时,y最小值=10.
所以,该农产品平均价格最低的是1月,最低为8元/千克.
(3)∵1至7月份的月平均价格呈一次函数,
∴x=4时的月平均价格17是前7个月的平均值.
将x=8,x=10和x=11分别代入y=x2-22x+131,得y=19,y=11和y=10.
∴后5个月的月平均价格分别为19,14,11,10,11.
∴年平均价格为
. |
| y |
| 17×7+19+14+11+10+11 |
| 12 |
| 46 |
| 3 |
当x=3时,y=14<15.3.
∴4,5,6,7,8这五个月的月平均价格高于年平均价格.
点评:本题考查了二次函数的应用,一次函数的应用.关键是根据函数图象,分段求出两个函数解析式,运用解析式解题.

练习册系列答案
相关题目
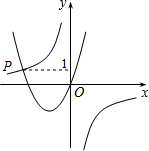 (2012•梁子湖区模拟)如图,已知函数
(2012•梁子湖区模拟)如图,已知函数 (2012•梁子湖区模拟)如图,DE是△ABC的中位线,M是DE的中点,CM的延长线交AB于N,且S△ABC=24,那么S四边形ANME-S△DMN=
(2012•梁子湖区模拟)如图,DE是△ABC的中位线,M是DE的中点,CM的延长线交AB于N,且S△ABC=24,那么S四边形ANME-S△DMN= (2012•梁子湖区模拟)如图,等腰梯形ABCD的底边AD在x轴上,顶点C在y轴正半轴上,B(4,2),一次函数y=kx-1的图象平分它的面积,关于x的函数y=mx2-(3m+k)x+2m+k的图象与坐标轴只有两个交点,则m的值为( )
(2012•梁子湖区模拟)如图,等腰梯形ABCD的底边AD在x轴上,顶点C在y轴正半轴上,B(4,2),一次函数y=kx-1的图象平分它的面积,关于x的函数y=mx2-(3m+k)x+2m+k的图象与坐标轴只有两个交点,则m的值为( )