题目内容
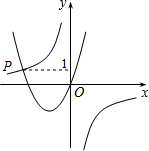 (2012•梁子湖区模拟)如图,已知函数y=-
(2012•梁子湖区模拟)如图,已知函数y=-| 3 |
| x |
| 3 |
| x |
x<-3或x>0
x<-3或x>0
.分析:所求不等式变形后,可以看做求二次函数的函数值大于反比例函数值时x的范围,由二次函数与反比例函数图象的交点,利用图象即可得到满足题意的x的范围,即为所求不等式的解集.
解答:解:∵反比例函数与二次函数图象交于点P,且P的纵坐标为1,
∴将y=1代入反比例函数y=-
得:x=-3,
∴P的坐标为(-3,1),
将所求的不等式变形得:ax2+bx>-
,
由图象可得:x<-3或x>0,
则关于x的不等式ax2+bx+
>0的解为x<-3或x>0.
故答案为:x<-3或x>0
∴将y=1代入反比例函数y=-
| 3 |
| x |
∴P的坐标为(-3,1),
将所求的不等式变形得:ax2+bx>-
| 3 |
| x |
由图象可得:x<-3或x>0,
则关于x的不等式ax2+bx+
| 3 |
| x |
故答案为:x<-3或x>0
点评:此题考查了二次函数与不等式(组),利用了数形结合的数学思想,数形结合是数学中的重要思想之一,解决函数问题更是如此,同学们要引起重视.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
 (2012•梁子湖区模拟)如图,DE是△ABC的中位线,M是DE的中点,CM的延长线交AB于N,且S△ABC=24,那么S四边形ANME-S△DMN=
(2012•梁子湖区模拟)如图,DE是△ABC的中位线,M是DE的中点,CM的延长线交AB于N,且S△ABC=24,那么S四边形ANME-S△DMN= (2012•梁子湖区模拟)如图,等腰梯形ABCD的底边AD在x轴上,顶点C在y轴正半轴上,B(4,2),一次函数y=kx-1的图象平分它的面积,关于x的函数y=mx2-(3m+k)x+2m+k的图象与坐标轴只有两个交点,则m的值为( )
(2012•梁子湖区模拟)如图,等腰梯形ABCD的底边AD在x轴上,顶点C在y轴正半轴上,B(4,2),一次函数y=kx-1的图象平分它的面积,关于x的函数y=mx2-(3m+k)x+2m+k的图象与坐标轴只有两个交点,则m的值为( )