Question

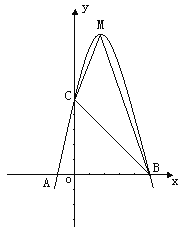
【题目】已知：二次函数y=ax2+bx+c的图象与x轴交于A、B两点，其中A点坐标为(-1，0)，点C(0，5)，另抛物线经过点(1，8)，M为它的顶点.

（1)求抛物线的解析式；

(2)求△MCB的面积S△MCB.

Answer 1

【答案】(1)y=－+4x+5；(2)15.

【解析】

试题分析：(1)、把三点代入函数解析式列出三元一次方程组，从而得出函数解析式；(2)、根据函数解析式求出点B和点M的坐标，然后作ME⊥y轴于点E，根据△MCB的面积=梯形EDBM的面积－△ECM的面积－△COB的面积得出答案.

试题解析：(1)依题意：

(2)令y=0，得(x-5)(x+1)=0，x1=5，x2=-1 ∴B(5，0)

由，得M(2，9) 作ME⊥y轴于点E，

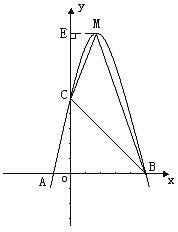
则 可得S△MCB=15.