题目内容
在直角坐标系中,如图所示,把∠BAC放在直角坐标系中,使射线AC与x轴重合,已知∠BAC=30°,OA=OB=1,过点B作BA1⊥OB交x轴于A1,过点A1做B1A1⊥BA1交直线AB于点B1,过B1做B1 A2⊥B1A1交x轴于点A2,再过A2依次作垂直….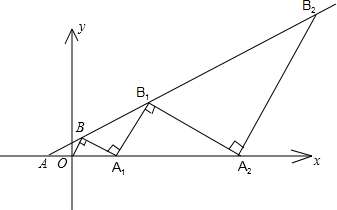
(1)求A、B点坐标(直接写出答案)
(2)求直线AB的解析式
(3)求△A6B6A7的面积.

(1)求A、B点坐标(直接写出答案)
(2)求直线AB的解析式
(3)求△A6B6A7的面积.
分析:(1)根据OA的长即可求出A的坐标,根据OB和∠BOA1=60°,即可求出B的坐标;
(2)设直线AB的解析式是y=kx+b,把A、B的坐标代入得出方程组,求出方程组的解即可;
(3)推出∠BAC=∠ABO=30°,求出∠BOC=60°,∠BA1O=30°,求出BA1=
,求出A1B1=
×
、B1A2=3
=
×
×
,同理求出A6B6=12个
相乘,B6A7=13个
相乘,根据三角形的面积公式求出即可.
(2)设直线AB的解析式是y=kx+b,把A、B的坐标代入得出方程组,求出方程组的解即可;
(3)推出∠BAC=∠ABO=30°,求出∠BOC=60°,∠BA1O=30°,求出BA1=
| 3 |
| 3 |
| 3 |
| 3 |
| 3 |
| 3 |
| 3 |
| 3 |
| 3 |
解答:(1)解:A(-1,0),B(
,
).
(2)解:设直线AB的解析式是:y=kx+b,
把A(-1,0),B(
,
)代入得:
,
解得:
,
∴直线AB的解析式为:y=
x+
.
(3)解:∵OB=OA=1,
∴∠BAC=∠ABO=30°,
∴∠BOC=60°,
∴∠BA1O=30°,
∴BA1=
,
同理∠BB1A1=30°,
∴B1A1=3=
×
,
同理:B1A2=3
=
×
×
,
…
A6B6=
×
×…×
(12个
相乘),
B6A7=
×
×…×
(13个
相乘),
∴△A6B6A7的面积是:
A6B6×B6A7=
×(
×
×…×
)×(
×
×…×
)=
,
答:△A6B6A7的面积是
.
| 1 |
| 2 |
| ||
| 2 |
(2)解:设直线AB的解析式是:y=kx+b,
把A(-1,0),B(
| 1 |
| 2 |
| ||
| 2 |
|
解得:
|
∴直线AB的解析式为:y=
| ||
| 3 |
| ||
| 3 |
(3)解:∵OB=OA=1,
∴∠BAC=∠ABO=30°,
∴∠BOC=60°,
∴∠BA1O=30°,
∴BA1=
| 3 |
同理∠BB1A1=30°,
∴B1A1=3=
| 3 |
| 3 |
同理:B1A2=3
| 3 |
| 3 |
| 3 |
| 3 |
…
A6B6=
| 3 |
| 3 |
| 3 |
| 3 |
B6A7=
| 3 |
| 3 |
| 3 |
| 3 |
∴△A6B6A7的面积是:
| 1 |
| 2 |
| 1 |
| 2 |
| 3 |
| 3 |
| 3 |
| 3 |
| 3 |
| 3 |
312
| ||
| 2 |
答:△A6B6A7的面积是
312
| ||
| 2 |
点评:本题考查了解直角三角形,含30度角的直角三角形,勾股定理等知识点的应用,关键是能根据求出的数据得出规律,题目比较好,但是有一定的难度.

练习册系列答案
相关题目
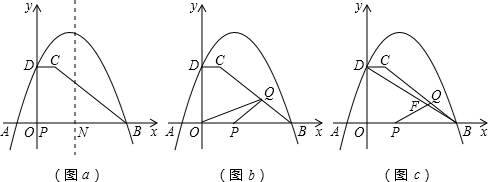
 (2013•吉安模拟)在直角坐标系中,如图有△ABC,现另有一点D满足以A、B、D为顶点的三角形与△ABC全等,则D点坐标为
(2013•吉安模拟)在直角坐标系中,如图有△ABC,现另有一点D满足以A、B、D为顶点的三角形与△ABC全等,则D点坐标为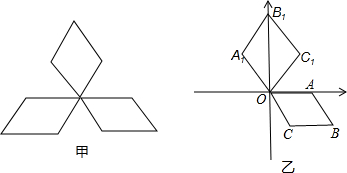
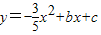 经过A、B、D三点,点G是抛物线的顶点,对称轴GH交x轴为H,动点P从点O沿OB以每秒1个单位的速度向终点B运动,设运动时间为t秒.
经过A、B、D三点,点G是抛物线的顶点,对称轴GH交x轴为H,动点P从点O沿OB以每秒1个单位的速度向终点B运动,设运动时间为t秒.