题目内容
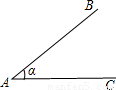
 如图,∠BAC=100°,点M在边BC上,△A′BC和△ABC对称于BC,△A′B′C和△A′BC对称于A′C,△A′B′C′和△A′B′C对称于A′B′,这时点M陆续变成M′和M″,那么∠MA′M″=
如图,∠BAC=100°,点M在边BC上,△A′BC和△ABC对称于BC,△A′B′C和△A′BC对称于A′C,△A′B′C′和△A′B′C对称于A′B′,这时点M陆续变成M′和M″,那么∠MA′M″=160°
160°
.分析:根据对称的性质可得,∠BAC=∠BA′C=∠B′A′C=∠100°,则可得出∠BA′B=160°,同理可得,∠BA′M=∠B′A′M′=∠B′A′M″,所以,∠BA′M″+∠B′A′M″=∠BA′M″+∠BA′M=160°,即可得出;
解答: 解:∵△A′BC和△ABC对称于BC,△A′B′C和△A′BC对称于A′C,△A′B′C′和△A′B′C对称于A′B′,∠BAC=100°,
解:∵△A′BC和△ABC对称于BC,△A′B′C和△A′BC对称于A′C,△A′B′C′和△A′B′C对称于A′B′,∠BAC=100°,
∴∠BAC=∠BA′C=∠B′A′C=∠B′A′C′=∠100°,
∴∠BA′B=360°-200°=160°,
∵点M在边BC上,点M陆续变成M′和M″,
同理得,∠BA′M=∠B′A′M′=∠B′A′M″,
∴∠BA′M″+∠B′A′M″=∠BA′M″+∠BA′M=160°,
即∠MA′M″=160°;
故答案为:160°.
 解:∵△A′BC和△ABC对称于BC,△A′B′C和△A′BC对称于A′C,△A′B′C′和△A′B′C对称于A′B′,∠BAC=100°,
解:∵△A′BC和△ABC对称于BC,△A′B′C和△A′BC对称于A′C,△A′B′C′和△A′B′C对称于A′B′,∠BAC=100°,∴∠BAC=∠BA′C=∠B′A′C=∠B′A′C′=∠100°,
∴∠BA′B=360°-200°=160°,
∵点M在边BC上,点M陆续变成M′和M″,
同理得,∠BA′M=∠B′A′M′=∠B′A′M″,
∴∠BA′M″+∠B′A′M″=∠BA′M″+∠BA′M=160°,
即∠MA′M″=160°;
故答案为:160°.
点评:本题主要考查了轴对称的性质和周角的性质,主要应用了轴对称图形的对应角相等.

练习册系列答案
相关题目
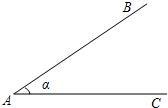 19、如图,∠BAC=30°,AB=10.现请你给定线段BC的长,使构成△ABC能惟一确定.你认为BC的长可以是
19、如图,∠BAC=30°,AB=10.现请你给定线段BC的长,使构成△ABC能惟一确定.你认为BC的长可以是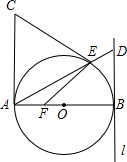 直线AE与l相交于点D.
直线AE与l相交于点D.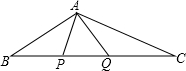 长为
长为