题目内容
(2004•郑州)如图,∠BAC=90°,AC=AB,直线l与以AB为直径的圆相切于点B,点E是圆上异于A、B的任意一点.直线AE与l相交于点D.(1)如果AD=10,BD=6,求DE的长;
(2)连接CE,过E作CE的垂线交直线AB于F.当点E在什么位置时,相应的F位于线段AB上、位于BA的延长线上、位于AB的延长线上(写出结果,不要求证明).无论点E如何变化,总有BD=BF.请你就上述三种情况任选一种说明理由.

【答案】分析:(1)由于DB是圆的切线,因此根据切割线定理得出的DB2=DE•DA即可求出DE的长;
(2)①设M是上半圆的中点,连接BC,AM,由于AB=AC,且∠CAB=90°,BC必过M点,连接AM则AM⊥BC,因此当E在BM弧上时,F在直径AB上.当E在AM弧上时,F在BA的延长线上.当E在下半圆时,F在AB的延长线上.
②本题可通过相似三角形来求解,由于∠CEA和∠FEB同是∠AEF的余角,因此这两角相等,根据弦切角定理可知:∠CAE=∠B,由此可得出,△CAE∽△FBE,同理可得出Rt△DBE∽Rt△BAE,那么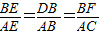 ,已知AC=AB,因此BD=BF.
,已知AC=AB,因此BD=BF.
解答: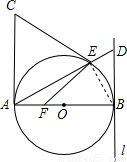 解:如图
解:如图
(1)∵BD是切线,DA是割线BD=6,AD=10
∴DB2=DE•DA
∴DE=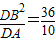 =3.6;
=3.6;
(2)设M是上半圆的中点,当E在BM弧上时,F在直径AB上
当E在AM弧上时,F在BA的延长线上,当E在下半圆时,F在AB的延长线上
连接BE
∵AB是直径,AC、BD是切线,∠CEF=90°
∴∠AEB=90°,∠CAE=∠FBE,∠DBE=∠BAE
∵∠CEA=90°-∠AEF
∠FEB=90°-∠AEF
∴∠CEA=∠FEB
∴Rt△DBE∽Rt△BAE,△CAE∽△FBE
∴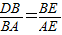 ,
,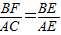
∵AC=AB
∴BD=BF.
点评:本题主要考查了切线的性质、切割线定理、圆周角定理、相似三角形的判定和性质等知识点.
(2)①设M是上半圆的中点,连接BC,AM,由于AB=AC,且∠CAB=90°,BC必过M点,连接AM则AM⊥BC,因此当E在BM弧上时,F在直径AB上.当E在AM弧上时,F在BA的延长线上.当E在下半圆时,F在AB的延长线上.
②本题可通过相似三角形来求解,由于∠CEA和∠FEB同是∠AEF的余角,因此这两角相等,根据弦切角定理可知:∠CAE=∠B,由此可得出,△CAE∽△FBE,同理可得出Rt△DBE∽Rt△BAE,那么
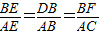 ,已知AC=AB,因此BD=BF.
,已知AC=AB,因此BD=BF.解答:
 解:如图
解:如图(1)∵BD是切线,DA是割线BD=6,AD=10
∴DB2=DE•DA
∴DE=
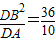 =3.6;
=3.6;(2)设M是上半圆的中点,当E在BM弧上时,F在直径AB上
当E在AM弧上时,F在BA的延长线上,当E在下半圆时,F在AB的延长线上
连接BE
∵AB是直径,AC、BD是切线,∠CEF=90°
∴∠AEB=90°,∠CAE=∠FBE,∠DBE=∠BAE
∵∠CEA=90°-∠AEF
∠FEB=90°-∠AEF
∴∠CEA=∠FEB
∴Rt△DBE∽Rt△BAE,△CAE∽△FBE
∴
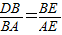 ,
,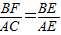
∵AC=AB
∴BD=BF.
点评:本题主要考查了切线的性质、切割线定理、圆周角定理、相似三角形的判定和性质等知识点.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目

 ,y=x+2,
,y=x+2,
 ,y=-x+2,
,y=-x+2,
 ,y=x-2,
,y=x-2,
 ,y=x-2,
,y=x-2,

 ,y=x+2,
,y=x+2,
 ,y=-x+2,
,y=-x+2,
 ,y=x-2,
,y=x-2,
 ,y=x-2,
,y=x-2,

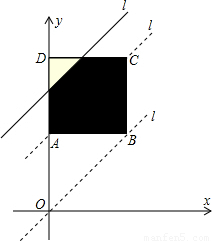

 ,y=x+2,
,y=x+2,
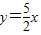 ,y=-x+2,
,y=-x+2,
 ,y=x-2,
,y=x-2,
 ,y=x-2,
,y=x-2,