题目内容
如图,△BAC中,∠BAC=100°,BC=10,AB的中垂线交BC于P,AC的中垂线交AC于Q,则△APQ的周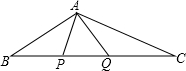 长为
长为
 长为
长为10
10
,∠PAQ=20°
20°
.分析:(1)根据线段垂直平分线上的点到线段两端点的距离相等AP=BP,AQ=CQ,所以△APQ的周长等于BC的长度;
(2)根据三角形内角和定理求出∠B+∠C=80°,再根据线段垂直平分线的性质求出∠BAP+∠CAQ=80°,则∠PAQ=∠BAC-80°.
(2)根据三角形内角和定理求出∠B+∠C=80°,再根据线段垂直平分线的性质求出∠BAP+∠CAQ=80°,则∠PAQ=∠BAC-80°.
解答:解:∵AB的中垂线交BC于P,AC的中垂线交AC于Q,
∴AP=BP,AQ=CQ,
∵BC=10,
∴△APQ的周长=AP+PQ+AQ=BP+PQ+CQ=BC=10;
∵∠BAC=100°,
∴∠B+∠C=180°-100°=80°,
∵AB的中垂线交BC于P,AC的中垂线交AC于Q,
∴∠BAP+∠CAQ=80°,
∴∠PAQ=100°-80°=20°.
故应填:10;20°.
∴AP=BP,AQ=CQ,
∵BC=10,

∴△APQ的周长=AP+PQ+AQ=BP+PQ+CQ=BC=10;
∵∠BAC=100°,
∴∠B+∠C=180°-100°=80°,
∵AB的中垂线交BC于P,AC的中垂线交AC于Q,
∴∠BAP+∠CAQ=80°,
∴∠PAQ=100°-80°=20°.
故应填:10;20°.
点评:本题主要考查线段垂直平分线的性质,熟练掌握性质是解题的关键.

练习册系列答案
 备战中考寒假系列答案
备战中考寒假系列答案
相关题目

 如图钢架BAC中,焊上等长的钢条来加固钢架,若P1A=P1P2,量得∠A=15°,则这样的钢管最多可以焊
如图钢架BAC中,焊上等长的钢条来加固钢架,若P1A=P1P2,量得∠A=15°,则这样的钢管最多可以焊 如图钢架BAC中,焊上等长的钢条p1p2,p2p3,p3p4,p4p5来加固钢架,若P1A=P1P2,则∠A的取值范围
如图钢架BAC中,焊上等长的钢条p1p2,p2p3,p3p4,p4p5来加固钢架,若P1A=P1P2,则∠A的取值范围