题目内容
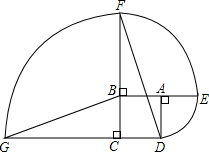 如图,ABCD是边长为1的正方形,其中
如图,ABCD是边长为1的正方形,其中 |
| DE |
 |
| EF |
 |
| FG |
(1)求点D沿三条圆弧运动到点G所经过的路线长;
(2)判断直线GB与DF的位置关系,并说明理由.
分析:本题考查的是弧长公式以及全等三角形的判定求出△FDC≌△GBC.
解答:解:(1)∵AD=1,∠DAE=90°,
∴
的长l1=
=
,
同理,
的长l2=
=π,
的长l3=
=
π,
所以,点D运动到点G所经过的路线长l=l1+l2+l3=3π.
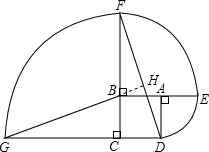
(2)直线GB⊥DF.
理由如下:延长GB交DF于H.
∵CD=CB,∠DCF=∠BCG,CF=CG,
∴△FDC≌△GBC.
∴∠F=∠G,
又∵∠F+∠FDC=90°,
∴∠G+∠FDC=90°,
即∠GHD=90°,
故GB⊥DF.
∴
 |
| DE |
| 90π×1 |
| 180 |
| π |
| 2 |
同理,
 |
| EF |
| 90π×2 |
| 180 |
 |
| FG |
| 90π×3 |
| 180 |
| 3 |
| 2 |
所以,点D运动到点G所经过的路线长l=l1+l2+l3=3π.

(2)直线GB⊥DF.
理由如下:延长GB交DF于H.
∵CD=CB,∠DCF=∠BCG,CF=CG,
∴△FDC≌△GBC.
∴∠F=∠G,
又∵∠F+∠FDC=90°,
∴∠G+∠FDC=90°,
即∠GHD=90°,
故GB⊥DF.
点评:求出弧长后可算出周长.“化曲面为平面”.

练习册系列答案
相关题目
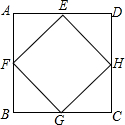 如图,ABCD是边长为1的正方形,EFGH是内接于ABCD的正方形,AE=a,AF=b,若SEFGH=
如图,ABCD是边长为1的正方形,EFGH是内接于ABCD的正方形,AE=a,AF=b,若SEFGH=| 2 |
| 3 |
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
 19、如图,ABCD是边长为6的正方形,请你建立一个适当的平面直角坐标系,并分别写出A、B、C、D的坐标.
19、如图,ABCD是边长为6的正方形,请你建立一个适当的平面直角坐标系,并分别写出A、B、C、D的坐标.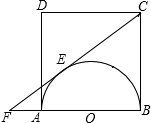 如图,ABCD是边长为2 a的正方形,AB为半圆O的直径,CE切⊙O于E,与BA的延长线交于F,求EF的长.
如图,ABCD是边长为2 a的正方形,AB为半圆O的直径,CE切⊙O于E,与BA的延长线交于F,求EF的长.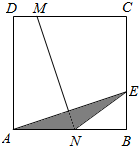 如图,ABCD是边长为9的正方形,E是BC上的一点,BE=
如图,ABCD是边长为9的正方形,E是BC上的一点,BE=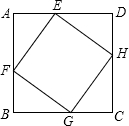 如图,ABCD是边长为1的正方形,EFGH是内接于ABCD的正方形,AE=a,AF=b,若正方形EFGH的面积为
如图,ABCD是边长为1的正方形,EFGH是内接于ABCD的正方形,AE=a,AF=b,若正方形EFGH的面积为