题目内容
 如图,ABCD是边长为1的正方形,EFGH是内接于ABCD的正方形,AE=a,AF=b,若SEFGH=
如图,ABCD是边长为1的正方形,EFGH是内接于ABCD的正方形,AE=a,AF=b,若SEFGH=| 2 |
| 3 |
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
分析:先求证△AEF≌△DHE得AF=DE,所以a+b=1,根据a+b=1,且a2+b2=
的等量关系求解.
| 2 |
| 3 |
解答:解:在△AEF和△DHE中,
,
∴△AEF≌△DHE,
∴AF=DE,
∵DE+AE=1,
∴a+b=1,
∵a2+b2=
求解得:a=
,b=
,
∴|b-a|=
,
故选 D.
|
∴△AEF≌△DHE,
∴AF=DE,
∵DE+AE=1,
∴a+b=1,
∵a2+b2=
| 2 |
| 3 |
求解得:a=
1+
| ||||
| 2 |
1-
| ||||
| 2 |
∴|b-a|=
| ||
| 3 |
故选 D.
点评:本题考查了全等三角形的判定,考查了正方形各边各角均相等的性质,解题的关键是证明△AEF≌△DHE,并找到条件a+b=1.

练习册系列答案
相关题目
 19、如图,ABCD是边长为6的正方形,请你建立一个适当的平面直角坐标系,并分别写出A、B、C、D的坐标.
19、如图,ABCD是边长为6的正方形,请你建立一个适当的平面直角坐标系,并分别写出A、B、C、D的坐标.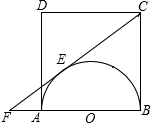 如图,ABCD是边长为2 a的正方形,AB为半圆O的直径,CE切⊙O于E,与BA的延长线交于F,求EF的长.
如图,ABCD是边长为2 a的正方形,AB为半圆O的直径,CE切⊙O于E,与BA的延长线交于F,求EF的长. 如图,ABCD是边长为9的正方形,E是BC上的一点,BE=
如图,ABCD是边长为9的正方形,E是BC上的一点,BE=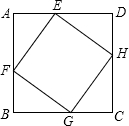 如图,ABCD是边长为1的正方形,EFGH是内接于ABCD的正方形,AE=a,AF=b,若正方形EFGH的面积为
如图,ABCD是边长为1的正方形,EFGH是内接于ABCD的正方形,AE=a,AF=b,若正方形EFGH的面积为