��Ŀ����
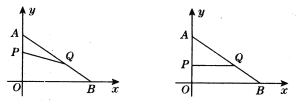
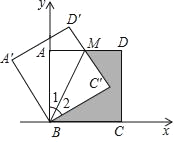
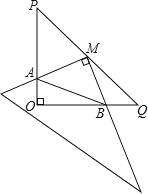
����Ŀ����ͼ���� Rt��POQ�У�OP=OQ=4��M �� PQ�е㣬��һ�����dz߶�����ڵ�M������MΪ��ת�ģ���ת���dzߣ����dzߵ���ֱ�DZ��� Rt��POQ����ֱ�DZ߷ֱ��ڵ�A��B��
��1����֤��MA=MB��
��2��̽��������ת���dzߵĹ����У��ı���AOBM������Ƿ����仯��Ϊʲô��
��3������ AB��̽��������ת���dzߵĹ����У���AOB���ܳ��Ƿ������Сֵ�������ڣ������Сֵ��
���𰸡���1������������2���ı��� AOBM �����û�з����仯�� ���ɼ���������3���� x=2 ʱ����AOB ���ܳ�����Сֵ����СֵΪ=4+2![]() ��
��
��������
��1������ M �� ME��OP �ڵ� E���� MF��OQ �ڵ� F�����������ε��ж������õ��ı��� OEMF �������Σ�֤����AME�ա�BMF������ȫ�������ε����ʽ��
��2������ȫ�������ε����ʵõ��ı��� AOBM �����=������ EOFM �������
��3������ȫ�������ε����ʵõ��õ� AE=BF���� OA=x�����ݹ��ɶ����õ�AB=![]() �����������ε��ܳ���ʽ�����κ��������ʽ��
�����������ε��ܳ���ʽ�����κ��������ʽ��
��1������ M �� ME��OP �ڵ� E���� MF��OQ �ڵ� F��
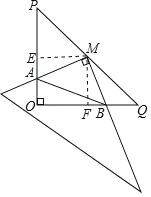
�ߡ�O=90�㣬��MEO=90�㣬��OFM=90�㣬
���ı��� OEMF �Ǿ��Σ�
��M �� PQ ���е㣬OP=OQ=4��
��ME=![]() OQ=2��MF=
OQ=2��MF=![]() OP=2��
OP=2��
��ME=MF��
���ı��� OEMF �������Σ�
�ߡ�AME+��AMF=90�㣬��BMF+��AMF=90�㣬
���AME=��BMF��
�ڡ�AME �͡�BMF �У�
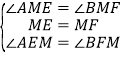
���AME�ա�BMF��ASA����
��MA=MB��
��2���ı��� AOBM �����û�з����仯�� �������£��ߡ�AME�ա�BMF��
���ı��� AOBM �����=������ EOFM �����=4��
��3���ߡ�AME�ա�BMF��
��AE=BF��
�� OA=x���� AE=2��x��
��OB=OF+BF=2+��2��x��=4��x��
�� Rt��AME ��AM=![]() =
= ![]() ��
��
�ߡ�AMB=90�㣬MA=MB��
��AB=![]() AM=
AM= ![]() ��
��
��AOB ���ܳ�=OA+OB+AB
=x+��4��x��+ ![]()
=4+![]() ��
��
�� x=2 ʱ����AOB ���ܳ�����Сֵ����СֵΪ=4+2![]() ��
��