题目内容
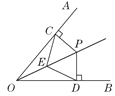
【题目】如图,OP为∠AOB的平分线,PC⊥OA,PD⊥OB,垂足分别是C,D,E为OP上一点,则下列结论错误的是( )
A. CE=DEB. ∠CPO=∠DEPC. ∠CEO=∠DEOD. OC=OD
【答案】B
【解析】
根据角平分线的性质得到PC=PD,进而根据HL证明Rt△PCO≌Rt△PDO可以判断B和D,再证明△COE≌△DOE,可以判断A和C.
∵OP为∠AOB的平分线,PC⊥OA,PD⊥OB,∴PC=PD.
在Rt△PCO和Rt△PDO中,∵PC=PD,PC=PC,∴Rt△PCO≌Rt△PDO,∴OC=OD,故D正确;
∵OC=OD,∠COP=∠DOP,OE=OE,∴△COE≌△DOE,∴CE=DE,故A正确;
∵Rt△PCO≌Rt△PDO,∴∠CPO=∠DPO,而∠CPO不一定等于∠DEP,∴无法判断∠CPO和∠DEP的大小关系,故B错误;
∵△COE≌△DOE,∴∠CEO=∠DEO,故C正确.
故选B.

练习册系列答案
相关题目