题目内容
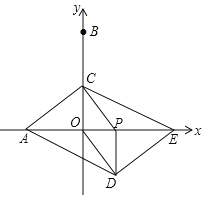
【题目】如图，在平面直角坐标系中，点A，B的坐标分别为（﹣3，0），（0，6）．动点P从点O出发，沿x轴正方向以每秒1个单位的速度运动，同时动点C从B出发，沿射线BO方向以每秒2个单位的速度运动，以CP，CO为邻边构造PCOD，在线段OP延长线上取点E，使PE=AO，设点P运动的时间为t秒．
（1）当点C运动到线段OB的中点时，求t的值及点E的坐标．
（2）当点C在线段OB上时，求证：四边形ADEC为平行四边形．
【答案】（1）t=
， E（
，0）；（2）见解析；
【解析】
（1）求出C是OB中点的时间，再求点E的坐标即可；
（2）连CD，由PCOD的对角线相等，证明四边形ADEC的对角线互相平分即可．
解：（1）∵OB=6，C是OB的中点，
∴BC=
OB=3，
∴2t=3即t=，
∴OE=+3=，E（，0）；
（2）如图，连接CD交OP于点G，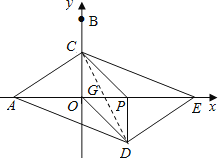
在PCOD中，CG=DG，OG=PG，
∵AO=PE，
∴AG=EG，
∴AE、CD互相平分
∴四边形ADEC是平行四边形．
练习册系列答案
相关题目
