题目内容
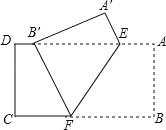
【题目】如图,正方形ABCD中,点E,F分别在边CD,BC上,且∠EAF=45°,BD分别交AE,AF于点M,N,以点A为圆心,AB长为半径画弧BD.下列结论:①DE+BF=EF;②BN2+DM2=MN2;③△AMN∽△AFE;④ ![]() 与EF相切;⑤EF∥MN.其中正确结论的个数是( )
与EF相切;⑤EF∥MN.其中正确结论的个数是( )
A.5个
B.4个
C.3个
D.2个
【答案】B
【解析】延长CB到G,使BG=DE,连接AG.

在△ABG和△ADE中,  ,
,
∴△ABG≌△ADE,
∴AG=AE,∠DAE=∠BAG,
又∵∠EAF=45°,∠DAB=90°,
∴∠DAE+∠BAF=45°
∴∠GAF=∠EAF=45°.
在△AFG和△AFE中,
 ,
,
∴△AFG≌△AFE,
∴GF=EF=BG+BF,
又∵DE=BG,
∴EF=DE+BF;故①正确;
在AG上截取AH=AM.
在△AHB和△AMD中,  ,
,
∴△AHB≌△AMD,
∴BH=DM,∠ABH=∠ADB=45°,
又∵∠ABD=45°,
∴∠HBN=90°.
∴BH2+BN2=HN2.
在△AHN和△AMN中,
 ,
,
∴△AHN≌△AMN,
∴MN=HN.
∴BN2+DM2=MN2;故②正确;
∵AB∥CD,
∴∠DEA=∠BAM.
∵∠AEF=∠AED,∠BAM=180°﹣∠ABM﹣∠AMN=180°﹣∠MAN﹣∠AMN=∠AND,
∴∠AEF=∠ANM,
又∠MAN=∠FAE,
∴△AMN∽△AFE,故③正确;
过A作AP⊥EF于P,
∵∠AED=∠AEP,AD⊥DE,
∴AP=AD,
∴ ![]() 与EF相切;故④正确;
与EF相切;故④正确;
∵∠ANM=∠AEF,而∠ANM不一定等于∠AMN,
∴∠AMN不一定等于∠AEF,
∴MN不一定平行于EF,故⑤错误,
所以答案是:B.
【考点精析】利用正方形的性质和切线的性质定理对题目进行判断即可得到答案,需要熟知正方形四个角都是直角,四条边都相等;正方形的两条对角线相等,并且互相垂直平分,每条对角线平分一组对角;正方形的一条对角线把正方形分成两个全等的等腰直角三角形;正方形的对角线与边的夹角是45o;正方形的两条对角线把这个正方形分成四个全等的等腰直角三角形;切线的性质:1、经过切点垂直于这条半径的直线是圆的切线2、经过切点垂直于切线的直线必经过圆心3、圆的切线垂直于经过切点的半径.