题目内容
【题目】如图,把矩形纸片ABCD沿EF折叠,使点B落在边AD上的点B′处,点A落在点A′处,已知AD=10,CD=4,B′D=2.
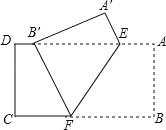
(1)求证:B′E=BF;
(2)求AE的长.
【答案】(1)证明见解析;(2)3.
【解析】
试题分析:(1)首先根据题意得B′F=BF,∠B′FE=∠BFE,接着根据平行线的性质和等腰三角形的判定即可证明B′E=BF;
(2)根据折叠的性质可得AE=A′E,AB=A′B′,在Rt△A′B′E中,根据勾股定理即可得到AE的长.
试题解析:(1)由题意得B′F=BF,∠B′FE=∠BFE,
在矩形ABCD中,AD∥BC,
∴∠B′EF=∠BFE,
∴∠B′FE=∠B′EF,
∴B′F=B′E,
∴B′E=BF;
(2)由折叠的性质可得AE=A′E,AB=A′B′=4,
在Rt△A′B′E中,A′B′2+A′E2=B′E2,
42+A′E2=(10-2-A′E)2,
解得A′E=3,
即AE的长为3.

练习册系列答案
相关题目