题目内容
如图,△ABC中, ,延长BA至D,使
,延长BA至D,使 ,点E、F分别是边BC、AC的中点.
,点E、F分别是边BC、AC的中点.

(1)判断四边形DBEF的形状并证明;
(2)过点A作AG⊥BC交DF于G,求证:AG=DG.
 ,延长BA至D,使
,延长BA至D,使 ,点E、F分别是边BC、AC的中点.
,点E、F分别是边BC、AC的中点.
(1)判断四边形DBEF的形状并证明;
(2)过点A作AG⊥BC交DF于G,求证:AG=DG.
(1)四边形 DBEF为等腰梯形,证明见解析;(2)证明见解析.
试题分析:(1)根据题意可知四边形DBEF是四边形;再证明BE=DE,即可判定四边形DBEF的形状;
(2)由四边形DBEF是等腰梯形知∠B=∠D,而AG∥BC,所以∠D=∠DAG,即可得AG=DG.
试题解析:(1)四边形 DBEF为等腰梯形,证明如下:

如图,过 F 作FH∥BC,交AB于H,
∵FH∥BC,点F是AC的中点,点E是BC的中点,
∴AH=BH=
 AB,EF∥AB.
AB,EF∥AB. 显然EF<AB<AD,∴EF≠AD
∴四边形DBEF为梯形
∵AD=
 AB
AB∴AD=AH
∵CA⊥AB
∴CA是DH的中垂线.
∴DF=FH
∵FH∥BC,EF∥AB
∴四边形HFEB是平等四边形.
∴FH=BE
∴BE=FD
故四边形 DBEF为等腰梯形
(2)∵四边形DBEF是等腰梯形
∴∠B=∠D
∵AG∥BC,∠B=∠DAG
∴∠D=∠DAG
∴AG=DG
考点: 等腰梯形的判定与性质.

练习册系列答案
 小学课时特训系列答案
小学课时特训系列答案
相关题目
 的外角,则
的外角,则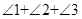 =
= 
 中,
中, 分别为边
分别为边 的中点,连接
的中点,连接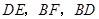 .
.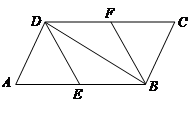
 .(4分)
.(4分) ,则四边形
,则四边形 是什么特殊四边形?请证明你的结论.(5分)
是什么特殊四边形?请证明你的结论.(5分)


