题目内容

如图所示的正方形网格中，每个小正方形的边长为1，以方格的格点作一个四边形，则四边形的四条边及两条对角线共六条线段中，其长度是无理数的有（　　）条．
分析：利用勾股定理分别求出六条线段的长，再根据无理数的概念进行解答即可．
解答：解：如图所示：
AB=AC=
52+52
=5
2
；
EF=
22+32
=
13
；
FG=
22+22
=2
2
；
GH=
22+22
=2
2
；
FH=
22+32
=
13
；
∵5
2
，
13
，2
2
均是无理数，故长度是无理数的有6条．
故选D．
点评：本题考查的是勾股定理，即在任何一个直角三角形中，两条直角边长的平方之和一定等于斜边长的平方．
练习册系列答案
相关题目
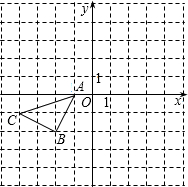精英家教网如图所示的正方形网格中，△ABC的顶点均在格点上，在所给直角坐标系中解答列问题：（1）分别写出点A、B两点的坐标；
（2）作出△ABC关于坐标原点成中心对称的△A1B1C1；
（3）求出△ABC的周长．（每个小正方形边长为1）
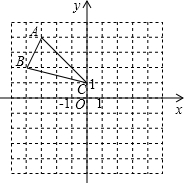精英家教网如图所示的正方形网格纸上，△ABC的顶点均在格点上，请解答下面几个问题：
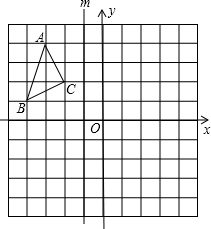（1）画出△A1B1C1，使△A1B1C1与△ABC关于y轴对称；画出△A2B2C2，使△A2B2C2与△ABC关于点O中心对称；
（2）分别写出B、B2两点的坐标；直线l恰经过B、B2两点，请画出直线l，并求出直线l的解析式．
如图所示的正方形网格中，每个小正方形的边长为1，△ABC的三个顶点都在格点上．
（1）写出△ABC顶点A的坐标，作出△ABC关于x轴对称的△A′B′C′．
（2）画出△ABC关于直线m对称的图形△A″B″C″，并写出点A″的坐标．
（3）计算出△ABC的面积．
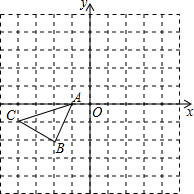如图所示的正方形网格中，△ABC的顶点均在格点上，在所给直角坐标系中解答下列问题：
（1）写出△ABC的三个顶点的坐标；
（2）画出△ABC关于x轴的对称图形△A′B′C′，并写出A′、B′、C′三点的坐标．
在如图所示的8×8正方形网格纸板上进行投针试验，随意向纸板投中一针，则投中阴影部分的概率是（　　）

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网