题目内容
 在同一平面直角坐标系中有6个点:A(1,1),B(-3,-1),C(-3,1),D(-2,-2),E(-2,-3),F(0,-4).
在同一平面直角坐标系中有6个点:A(1,1),B(-3,-1),C(-3,1),D(-2,-2),E(-2,-3),F(0,-4).(1)画出△ABC的外接圆⊙P,并指出点D与⊙P的位置关系;
(2)画出直线EF并把直线EF沿y轴向上平移,使它经过点D,设此时的直线为l1.请判断直线l1与⊙P的位置关系,并说明理由.
分析:(1)根据A、B、C的坐标可得到△ABC为直角三角形,则AB为△ABC外接圆⊙P的直径,AB的中点P的坐标为(-1,0),利用勾股定理计算出AB,得到⊙P的半径=
AB=
,再利用勾股定理计算出PD=
,然后根据点与圆的位置关系进行判断;
(2)由于D(-2,-2),E(-2,-3),F(0,-4),则直线EF沿y轴向上平移,使它经过点D,得到直线EF向上平移1个单位得到l1,则点F平移到Q点(0,-3),再利用勾股定理可计算出PD2=5,DF2=22+12=5,PQ2=12+32=10,然后根据勾股定理的逆定理得到∠PDQ=90°,再根据圆的切线的判定定理即可得到直线l1与⊙P相切.
| 1 |
| 2 |
| 5 |
| 5 |
(2)由于D(-2,-2),E(-2,-3),F(0,-4),则直线EF沿y轴向上平移,使它经过点D,得到直线EF向上平移1个单位得到l1,则点F平移到Q点(0,-3),再利用勾股定理可计算出PD2=5,DF2=22+12=5,PQ2=12+32=10,然后根据勾股定理的逆定理得到∠PDQ=90°,再根据圆的切线的判定定理即可得到直线l1与⊙P相切.
解答: 解:(1)∵A(1,1),B(-3,-1),C(-3,1),
解:(1)∵A(1,1),B(-3,-1),C(-3,1),
∴BC∥y轴,AC∥x轴,
∴BC⊥AC,
∴△ABC为直角三角形,
∴AB为△ABC外接圆⊙P的直径,AB的中点P的坐标为(-1,0),
⊙P的半径=
AB=
=
=
,
∵PD=
=
,
∴点D在⊙P上;
(2)直线l1与⊙P相切.理由如下:
∵D(-2,-2),E(-2,-3),F(0,-4),
∴直线EF沿y轴向上平移,使它经过点D,即直线EF向上平移1个单位得到l1,
∴点F平移到Q点(0,-3),如图,
连接PQ,PD2=5,DF2=22+12=5,PQ2=12+32=10,
∴PD2+DF2=PQ2,
∴∠PDQ=90°,
∴直线l1与⊙P相切.
 解:(1)∵A(1,1),B(-3,-1),C(-3,1),
解:(1)∵A(1,1),B(-3,-1),C(-3,1),∴BC∥y轴,AC∥x轴,
∴BC⊥AC,
∴△ABC为直角三角形,
∴AB为△ABC外接圆⊙P的直径,AB的中点P的坐标为(-1,0),
⊙P的半径=
| 1 |
| 2 |
| 1 |
| 2 |
| AC2+BC2 |
| 1 |
| 2 |
| 42+22 |
| 5 |
∵PD=
| 12+22 |
| 5 |
∴点D在⊙P上;
(2)直线l1与⊙P相切.理由如下:
∵D(-2,-2),E(-2,-3),F(0,-4),
∴直线EF沿y轴向上平移,使它经过点D,即直线EF向上平移1个单位得到l1,
∴点F平移到Q点(0,-3),如图,
连接PQ,PD2=5,DF2=22+12=5,PQ2=12+32=10,
∴PD2+DF2=PQ2,
∴∠PDQ=90°,
∴直线l1与⊙P相切.
点评:本题考查了圆的综合题:熟练掌握点与圆的位置关系和直线与圆相切的判定方法;记住直角三角形外接圆的圆心为斜边的中点;会根据勾股定理计算平面直角坐标系中两点的距离.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
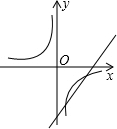
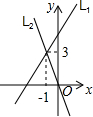 直线L1:y=2x+5与直线L2:y=kx+b在同一平面直角坐标系中的图象如图,则关于x的不等式2x+5<kx+b的解集为( )
直线L1:y=2x+5与直线L2:y=kx+b在同一平面直角坐标系中的图象如图,则关于x的不等式2x+5<kx+b的解集为( )