题目内容
已知,如图:Rt△ABC中,∠ABC=90°,AB=8,BC=10,D为△ABC外一点,连接AD,BD,过D作DH⊥AB,垂 足为H,交AC于E.
足为H,交AC于E.
(1)若△ABD是等边三角形,求DE的长为________;
(2)若BD=AB,且tan∠HDB= ,求DE的长为________.
,求DE的长为________.
(根据2007年重庆中考题改编)
解:(1)∵△ABD是等边三角形,
∴DH垂直平分AB且∠ADH=30°,
∴EH是△ABC的中位线,
∵AB=8,BC=10,
∴DH=4 ,EH=5,
,EH=5,
∴DE=4 -5;
-5;
(2)∵BD=AB,tan∠HDB= ,AB=8,DH⊥AB,
,AB=8,DH⊥AB,
∴在Rt△BDH中,DH=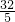 ,BH=
,BH=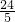 ,
,
∵AB=8,
∴AH=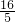 ,
,
∵DH⊥AB,
∴△AHE∽△ABC,
∴AH:AB=EH:BC,
即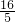 :8=EH:10,
:8=EH:10,
∴EH=4,
∴DE=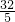 -4=
-4= .
.
分析:(1)利用等边三角形的性质及中位线就可求得DE的长;
(2)DH⊥AB,可证△AHE∽△ABC,利用相似比可计算EH的长,则DE的长可求解.
点评:本题主要考查了等边三角形的性质及相似三角形的判定及性质.
∴DH垂直平分AB且∠ADH=30°,
∴EH是△ABC的中位线,
∵AB=8,BC=10,
∴DH=4
 ,EH=5,
,EH=5,∴DE=4
 -5;
-5;(2)∵BD=AB,tan∠HDB=
 ,AB=8,DH⊥AB,
,AB=8,DH⊥AB,∴在Rt△BDH中,DH=
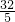 ,BH=
,BH=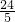 ,
,∵AB=8,
∴AH=
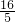 ,
,∵DH⊥AB,
∴△AHE∽△ABC,
∴AH:AB=EH:BC,
即
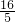 :8=EH:10,
:8=EH:10,∴EH=4,
∴DE=
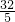 -4=
-4= .
.分析:(1)利用等边三角形的性质及中位线就可求得DE的长;
(2)DH⊥AB,可证△AHE∽△ABC,利用相似比可计算EH的长,则DE的长可求解.
点评:本题主要考查了等边三角形的性质及相似三角形的判定及性质.

练习册系列答案
相关题目
 22、已知:如图,Rt△ABC≌Rt△ADE,∠ABC=∠ADE=90°,试以图中标有字母的点为端点,连接两条线段,如果你所连接的两条线段满足相等,垂直或平行关系中的一种,那么请你把它写出来并证明.
22、已知:如图,Rt△ABC≌Rt△ADE,∠ABC=∠ADE=90°,试以图中标有字母的点为端点,连接两条线段,如果你所连接的两条线段满足相等,垂直或平行关系中的一种,那么请你把它写出来并证明.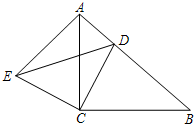 20、已知:如图,Rt△ABC中,∠ACB=90°,AC=BC,点D为AB边上一点,且不与A、B两点重合,AE⊥AB,AE=BD,连接DE、DC.
20、已知:如图,Rt△ABC中,∠ACB=90°,AC=BC,点D为AB边上一点,且不与A、B两点重合,AE⊥AB,AE=BD,连接DE、DC.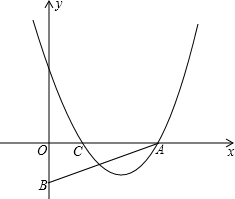 C=OB,抛物线y=(x-2)(x-m)-(p-2)(p-m)(m、p为常数且m+2≥2p>0)经过A、C两点.
C=OB,抛物线y=(x-2)(x-m)-(p-2)(p-m)(m、p为常数且m+2≥2p>0)经过A、C两点.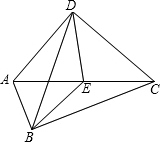 已知:如图,Rt△ABC和Rt△ADC,∠ABC=∠ADC=90°,点E是AC的中点.
已知:如图,Rt△ABC和Rt△ADC,∠ABC=∠ADC=90°,点E是AC的中点.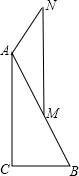 已知:如图,Rt△ABC中,∠C=90°,M是AB的中点,AM=AN,MN∥AC.
已知:如图,Rt△ABC中,∠C=90°,M是AB的中点,AM=AN,MN∥AC.