题目内容
 20、已知:如图,Rt△ABC中,∠ACB=90°,AC=BC,点D为AB边上一点,且不与A、B两点重合,AE⊥AB,AE=BD,连接DE、DC.
20、已知:如图,Rt△ABC中,∠ACB=90°,AC=BC,点D为AB边上一点,且不与A、B两点重合,AE⊥AB,AE=BD,连接DE、DC.(1)求证:△ACE≌△BCD;
(2)猜想:△DCE是
等腰直角
三角形;并说明理由.分析:(1)由已知可得△ABC是等腰直角三角形,由AE⊥AB即可得到∠1=∠B,从而可利用SAS判定△ACE≌△BCD.
(2)根据已知可猜想其为等腰直角三角形,由第一问可得CE=CD,∠3=∠4,根据等角的性质可推出∠ECD=90°,从而即得到了答案.
(2)根据已知可猜想其为等腰直角三角形,由第一问可得CE=CD,∠3=∠4,根据等角的性质可推出∠ECD=90°,从而即得到了答案.
解答: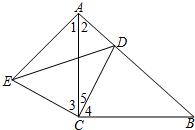 (1)证明:
(1)证明:
∵∠ACB=90°,AC=BC,
∴∠B=∠2=45°.
∵AE⊥AB,
∴∠1+∠2=90°.
∴∠1=45°.
∴∠1=∠B.
∵AE=BD,AC=BC,
∴△ACE≌△BCD.
(2)猜想:△DCE是等腰直角三角形;
理由说明:
∵△ACE≌△BCD,
∴CE=CD,∠3=∠4.
∵∠4+∠5=90°,
∴∠3+∠5=90°.
即∠ECD=90°.
∴△DCE是等腰直角三角形.
 (1)证明:
(1)证明:∵∠ACB=90°,AC=BC,
∴∠B=∠2=45°.
∵AE⊥AB,
∴∠1+∠2=90°.
∴∠1=45°.
∴∠1=∠B.
∵AE=BD,AC=BC,
∴△ACE≌△BCD.
(2)猜想:△DCE是等腰直角三角形;
理由说明:
∵△ACE≌△BCD,
∴CE=CD,∠3=∠4.
∵∠4+∠5=90°,
∴∠3+∠5=90°.
即∠ECD=90°.
∴△DCE是等腰直角三角形.
点评:此题主要考查学生对全等三角形的判定方法及等腰直角三角形的判定的综合运用.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
 22、已知:如图,Rt△ABC≌Rt△ADE,∠ABC=∠ADE=90°,试以图中标有字母的点为端点,连接两条线段,如果你所连接的两条线段满足相等,垂直或平行关系中的一种,那么请你把它写出来并证明.
22、已知:如图,Rt△ABC≌Rt△ADE,∠ABC=∠ADE=90°,试以图中标有字母的点为端点,连接两条线段,如果你所连接的两条线段满足相等,垂直或平行关系中的一种,那么请你把它写出来并证明.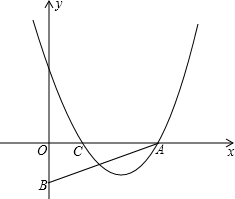 C=OB,抛物线y=(x-2)(x-m)-(p-2)(p-m)(m、p为常数且m+2≥2p>0)经过A、C两点.
C=OB,抛物线y=(x-2)(x-m)-(p-2)(p-m)(m、p为常数且m+2≥2p>0)经过A、C两点.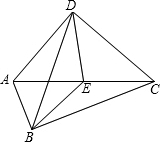 已知:如图,Rt△ABC和Rt△ADC,∠ABC=∠ADC=90°,点E是AC的中点.
已知:如图,Rt△ABC和Rt△ADC,∠ABC=∠ADC=90°,点E是AC的中点.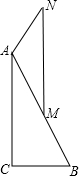 已知:如图,Rt△ABC中,∠C=90°,M是AB的中点,AM=AN,MN∥AC.
已知:如图,Rt△ABC中,∠C=90°,M是AB的中点,AM=AN,MN∥AC.