题目内容
【题目】已知:如图,在Rt△ABC中,∠ACB=90°,点D在边AC上,点E是BD的中点,CE的延长线交边AB于点F,且∠CED=∠A. 
(1)求证:AC=AF;
(2)在边AB的下方画∠GBA=∠CED,交CF的延长线于点G,联结DG,在图中画出图形,并证明四边形CDGB是矩形.
【答案】
(1)证明:∵∠BCD=90°,DE=EB,
∴EC=ED=EB,
∴∠EDC=∠ECD,
∵∠CED+∠CDE+∠DCE=180°,∠A+∠DCE+∠AFC=180°,
又∵∠CED=∠A,
∴∠CDE=∠AFC,
∴∠AFC=∠ACF,
∴AC=AF
(2)解:图象如图所示.
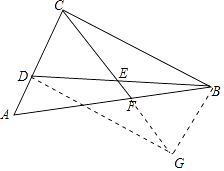
∵∠CED=∠ABG,∠CED=∠A,
∴∠A=∠ABG,
∴AC∥BG,
∴∠ECD=∠BGE,
在△CED和△GEB中,
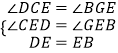 ,
,
∴△CED≌△GEB,
∴CE=EG,
∴CE=DE=EB,
∴CG=BD,CE=EG,DE=EB,
∴四边形CDGB是平行四边形,∵BD=CG,
∴四边形CDGB是矩形
【解析】(1)只要证明∠CDE=∠ECD,∠CDE=∠AFC即可解决问题.(2)只要证明CG=BD,CE=EG,DE=EB即可.
【考点精析】利用矩形的判定方法和相似三角形的判定与性质对题目进行判断即可得到答案,需要熟知有一个角是直角的平行四边形叫做矩形;有三个角是直角的四边形是矩形;两条对角线相等的平行四边形是矩形;相似三角形的一切对应线段(对应高、对应中线、对应角平分线、外接圆半径、内切圆半径等)的比等于相似比;相似三角形周长的比等于相似比;相似三角形面积的比等于相似比的平方.

练习册系列答案
 夺冠训练单元期末冲刺100分系列答案
夺冠训练单元期末冲刺100分系列答案 新思维小冠军100分作业本系列答案
新思维小冠军100分作业本系列答案 名师指导一卷通系列答案
名师指导一卷通系列答案
相关题目