题目内容
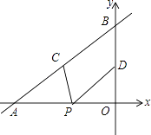
【题目】如图，在平面直角坐标系xOy中，直线y=﹣2x+a与y轴交于点C （0，6），与x轴交于点B．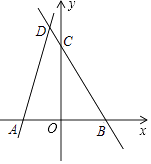 
（1）求这条直线的解析式；
（2）直线AD与（1）中所求的直线相交于点D（﹣1，n），点A的坐标为（﹣3，0）． ①求n的值及直线AD的解析式；
②求△ABD的面积；
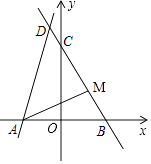
③点M是直线y=﹣2x+a上的一点（不与点B重合），且点M的横坐标为m，求△ABM的面积S与m之间的关系式．
【答案】
（1）解：∵直线y=﹣2x+a与y轴交于点C （0，6），
∴a=6，
∴该直线解析式为y=﹣2x+6
（2）解：①∵点D（﹣1，n）在直线BC上，
∴n=﹣2×（﹣1）+6=8，
∴点D（﹣1，8）．）
设直线AD的解析式为y=kx+b，
将点A（﹣3，0）、D（﹣1，8）代入y=kx+b中，
得： 
，
解得： 
，
∴直线AD的解析式为y=4x+12．
②令y=﹣2x+6中y=0，则﹣2x+6=0，解得：x=3，
∴点B（3，0）．
∵A（﹣3，0）、D（﹣1，8），
∴AB=6．
S△ABD= 
AByD= ×6×8=24．
③∵点M在直线y=﹣2x+6上，
∴M（m，﹣2m+6），
则 
当m＜3时，S= 
即S=﹣6m+18；
当m＞3时， 
即S=6m﹣18．
【解析】（1）将点C（0，6）代入y=﹣2x+a求得a的值即可；（2）①将点D坐标代入直线BD解析式可得n的值，再利用待定系数法可求得直线AD解析式；②根据三角形面积公式即可得；③设M（m，﹣2m+6），根据面积公式可得函数关系式．
【题目】（本题8分） 求一个正数的算术平方根，有些数可以直接求得，如
，有些数则不能直接求得，如
，但可以通过计算器求. 还有一种方法可以通过一组数的内在联系，运用规律求得，请同学们观察下表：
n | 16 | 0.16 | 0.0016 | 1600 | 160000 | … |
| 4 | 0.4 | 0.04 | 40 | 400 | … |
（1）表中所给的信息中，你能发现什么规律？（请将规律用文字表达出来）
（2）运用你发现的规律，探究下列问题：已知
1．435，求下列各数的算术平方根：
①0.0206 ； ②20600 ；
（3）根据上述探究过程类比研究一个数的立方根已知
1.260，则
