题目内容
【题目】抛物线y=ax2+bx+c（a≠0）过点A（1，﹣3）、B（3，﹣3）、C（﹣1，5），顶点为M点．在抛物线上是找一点P使∠POM=90°，则P点的坐标_____．
【答案】（
，
）
【解析】
根据题意，把抛物线经过的三点代入函数的表达式，列出方程组，解出各系数，再确抛物线的顶点M的坐标．可求出直线OM的解析式，由于直线OP与直线PM垂直，因此两直线的斜率的积为1，由此可求出直线OP的解析式；联立抛物线的解析式即可求出P点坐标．
抛物线y＝ax2＋bx＋c（a≠0）过点A（1，3）、B（3，3）、C（1，5），
所以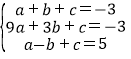
，解得：
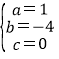
所以抛物线的解析式为：y＝x24x＝（x2）24，顶点M坐标是（2，4），
因此直线OM的解析式为y＝2x，
由于直线PO与直线OM垂直，因此直线PO的解析式为y＝
x，
联立抛物线的解析式有：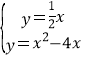
，
解得
，
因此P点坐标为（，）．
故答案为：（，）
练习册系列答案
世纪百通期末金卷系列答案
相关题目
