题目内容
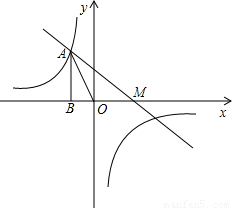
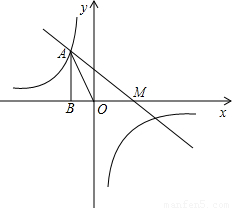
(2005•呼和浩特)如图,已知反比例函数y=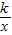 的图象经过点A(-
的图象经过点A(-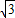 ,b),过点A作AB⊥x轴,垂足为点B,△AOB的面积为
,b),过点A作AB⊥x轴,垂足为点B,△AOB的面积为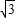 .
.(1)求k和b的值;
(2)若一次函数y=ax+1的图象经过点A,并且与x轴相交于点M,求OA:OM.
【答案】分析:(1)根据点A(-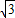 ,b)知OB=
,b)知OB=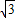 ,由△AOB的面积为
,由△AOB的面积为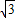 求出b,再由A点坐标求出k;
求出b,再由A点坐标求出k;
(2)由一次函数y=ax+1的图象经过点A求出a,得函数解析式,再求M的坐标,得OM的长;在△AOB中求OA的长,最后求比值.
解答:解:(1)根据题意得: ×
×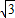 b=
b=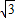 ,b=2,
,b=2,
∴A(-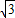 ,2)因为反比例函数y=
,2)因为反比例函数y= 的图象经过点A,
的图象经过点A,
∴k=-2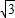 ;
;
(2)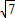 :
: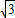 .
.
∵一次函数y=ax+1的图象经过点A,
∴-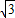 a+1=2,a=-
a+1=2,a=- ,函数解析式为y=-
,函数解析式为y=-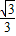 x+1,
x+1,
当y=0时,x=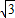 ,即OM=
,即OM=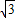 ,
,
在Rt△AOB中,OA=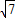 ,
,
∴OA:OM=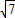 :
: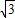 .
.
点评:此题重在检测函数解析式的求法及交点的求法.解答本题时同学们要结合图象,正确解答.
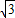 ,b)知OB=
,b)知OB=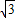 ,由△AOB的面积为
,由△AOB的面积为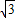 求出b,再由A点坐标求出k;
求出b,再由A点坐标求出k;(2)由一次函数y=ax+1的图象经过点A求出a,得函数解析式,再求M的坐标,得OM的长;在△AOB中求OA的长,最后求比值.
解答:解:(1)根据题意得:
 ×
×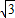 b=
b=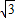 ,b=2,
,b=2,∴A(-
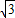 ,2)因为反比例函数y=
,2)因为反比例函数y= 的图象经过点A,
的图象经过点A,∴k=-2
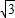 ;
;(2)
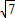 :
: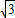 .
.∵一次函数y=ax+1的图象经过点A,
∴-
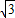 a+1=2,a=-
a+1=2,a=- ,函数解析式为y=-
,函数解析式为y=-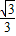 x+1,
x+1,当y=0时,x=
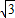 ,即OM=
,即OM=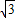 ,
,在Rt△AOB中,OA=
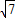 ,
,∴OA:OM=
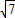 :
: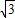 .
.点评:此题重在检测函数解析式的求法及交点的求法.解答本题时同学们要结合图象,正确解答.

练习册系列答案
相关题目
(2005•呼和浩特)2006年世界杯足球赛预计现场观看人数将达到1 820 000人,用科学记数法表示为( )
A.1.82×105人
B.0.182×107人
C.1.82×106人
D.182×104人
A.1.82×105人
B.0.182×107人
C.1.82×106人
D.182×104人
(2005•呼和浩特)某商场搞“真情回报社会”的幸运抽奖活动,最高奖金为每份l万元,平均奖金180元.下面是奖金的分配表:
一名顾客抽到一张奖券,奖金数为10元,她调查了周围不少正在兑奖的其他顾客,很少有超过50元的,她气愤地去找商场的领导理论,领导解释说这不存在什么欺骗,平均奖金确实是180元,你认为商场所说的平均奖金是否欺骗了顾客?此种说法是否能够很好地反映中奖的一般金额?用你所学的统计与概率的有关知识做简要分析说明.以后再遇上类似抽奖活动的问题,你会更关心什么?
| 奖金等级 | 一等奖 | 二等奖 | 三等奖 | 四等奖 | 五等奖 |
| 奖金额(元) | 10000 | 5000 | 1000 | 50 | 10 |
| 中奖人数 | 3 | 8 | 89 | 300 | 600 |
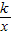 的图象经过点A(-
的图象经过点A(-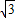 ,b),过点A作AB⊥x轴,垂足为点B,△AOB的面积为
,b),过点A作AB⊥x轴,垂足为点B,△AOB的面积为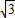 .
.
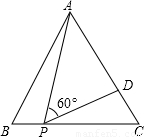
 ,则△ABC的边长为( )
,则△ABC的边长为( )