题目内容
【题目】在锐角△ABC中,∠BAC=60,BD、CE为高,F为BC的中点,连接DE、DF、EF,则结论:①DF=EF;②AD∶AB=AE∶AC;③△DEF是等边三角形;④BE+CD=BC;⑤当∠ABC=45时,BE=![]() DE中,一定正确的有 .
DE中,一定正确的有 . 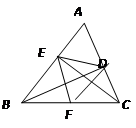
【答案】①②③⑤
【解析】解:①∵BD、CE为高,∴△BEC、△BDC是直角三角形.
∵F是BC的中点,∴EF=DF= ![]() BC.①正确;
BC.①正确;
②∵∠ADB=∠AEC=90°,∠A公共,∴△ABD∽△ACE,得AD:AB=AE:AC.②正确;
③∵∠A=60°,∴∠ABC+∠ACB=120°.
∵F是BC的中点,∴EF=BF,DF=CF.∴∠ABF=∠BEF,∠ACB=∠CDF.
∴∠BFE+∠CFD=120°,∠EFD=60°.又∵EF=FD,∴△DEF是等边三角形.③正确;
④若BE+CD=BC,则可在BC上截取BH=BE,则HC=CD.
∵∠A=60°,∴∠ABC+∠ACB=120°.又∵BH=BE,HC=CD,
∴∠BHE+∠CHD=120°,∠EHD=60°.
所以存在满足条件的点,假设成立,但一般情况不一定成立,故错误;
⑤∵∠ABC=45°,∴BE= ![]() BC=
BC= ![]() DE.
DE.
故答案为①②③⑤
利用直角三角形的斜边中线定理可得EF=DF= ![]() BC;可证出△ABD∽△ACE,得AD:AB=AE:AC;由∠BFE+∠CFD=360°-120°-120°=120°,可知∠EFD=60°.又∵EF=FD,∴△DEF是等边三角形;可采用反证法得出④错误;若∠ABC=45°,可得BE=
BC;可证出△ABD∽△ACE,得AD:AB=AE:AC;由∠BFE+∠CFD=360°-120°-120°=120°,可知∠EFD=60°.又∵EF=FD,∴△DEF是等边三角形;可采用反证法得出④错误;若∠ABC=45°,可得BE= ![]() BC=
BC= ![]() DE.
DE.

练习册系列答案
 夺冠金卷全能练考系列答案
夺冠金卷全能练考系列答案
相关题目