Question

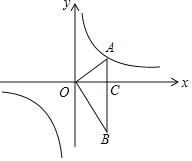
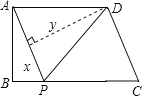
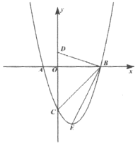
【题目】如图，已知抛物线与x轴交于A、B两点，与y轴交于点C，点为抛物线的顶点，且．

（1）求抛物线的解析式；

（2）设，，求的值；

（3）探究坐标轴上是否存在点P，使得以P、A、C三点为顶点的三角形与相似，若存在，请指出点P的位置，并直接写出点P的坐标，若不存在，请说明理由．

Answer 1

【答案】（1）；（2）；（3）存在，，，

【解析】

（1）将点A、E的坐标代入抛物线解析式求出a、b即可；

（2）首先求出BD、EC、BC、BE的长，证明得出，将求的值转化为求的值，计算即可；

（3）首先证明∠ACO＝∠EBC，∠OAC＝∠CEB，可得以P、A、C三点为顶点与相似的三角形必为直角三角形，然后分情况讨论：①以A为直角顶点时，②以C为直角顶点时，③以Р为直角顶点时，利用射影定理求出OP的长即可.

解：（1）将，代入可得，

解得：

∴抛物线的解析式为：；

（2）∵，，

∴，

令，

解得：，，

∴，

∵，，

∴，，，，

∵，，，

∴，

∴，

∴，

∴；

（3）∵OA=OD=1，OC=OB=3，∠AOC＝∠DOB，

∴△AOC≌△DOB，

∴∠ACO＝∠DBO，∠OAC＝∠ODB，

∵，

∴∠DBO＝∠EBC，∠ODB＝∠CEB，

∴∠ACO＝∠EBC，∠OAC＝∠CEB，

∵为直角三角形，则以P、A、C三点为顶点与相似的三角形必为直角三角形，

∴分三种情况讨论：

①以A为直角顶点时，

在中，，即：，

∴，

∴；

②以C为直角顶点时，在中，，即：，

∴，

∴；

③以Р为直角顶点时，则P与O重合，

即；

综上所述：满足条件的Р点有，，．