题目内容
如图,在直角三角形ABC和直角三角形ADE中,AB=AC,AD=AE,CE与BD交于点M,BD交AC于N.
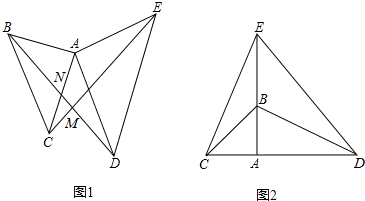
①求证:BD=CE;
②求证:BD⊥CE;
③当三角形ABC绕点A顺时针方向旋转到如图②的位置时,上述结论是否成立?请选择一个结论给予证明.
①证明:∵△ABC和△ADE是等腰直角三角形,
∴∠BAC=∠EAD=90°,
∴∠BAC+∠CAD=∠EAD+∠CAD,
即∠BAD=∠EAC,
∵在△BAD和△CAE中
 ,
,
∴△BAD≌△CAE(SAS),
∴BD=CE;
②证明:∵△BAD≌△CAE,
∴∠AEC=∠ADB,
∵∠EAD=90°,
∴∠1+∠AEC=90°,
∵∠1=∠2,
∴∠2+∠ADB=90°,
∴∠DME=180°-90°=90°,
∴BD⊥CE;
③解:当三角形ABC绕点A顺时针方向旋转到如图②的位置时,上述结论还成立,
理由是:延长DB交CE于F,
∵在△BAD和△CAE中
 ,
,
∴△BAD≌△CAE(SAS),
∴BD=CE,∠AEC=∠ADB,
∵∠EAD=90°,
∴∠4+∠ADB=90°,
∵∠3=∠4,
∴∠3+∠AEC=90°,
∴∠5=180°-90°=90°,
∴BD⊥CE,
即当三角形ABC绕点A顺时针方向旋转到如图②的位置时,上述结论还成立.
分析:①根据直角三角形性质得出∠BAC=∠EAD=90°,推出∠BAD=∠EAC,根据SAS证△BAD≌△CAE,推出BD=CE即可;
②根据全等三角形的性质推出∠AEC=∠ADB,根据∠1+∠AEC=90°推出∠2+∠ADB=90°,求出∠DME=90°,根据垂直定义求出即可;
③延长DB交CE于F,根据SAS证△BAD≌△CAE,推出BD=CE,∠AEC=∠ADB,求出∠3+∠AEC=90°,求出∠5=90°,根据垂直定义求出即可.
点评:本题考查了全等三角形的性质和判定,垂直定义,三角形的内角和定理等知识点,通过做此题培养了学生的猜想能力和推理能力,题目具有一定的代表性,是一道比较好的题目.
∴∠BAC=∠EAD=90°,
∴∠BAC+∠CAD=∠EAD+∠CAD,
即∠BAD=∠EAC,
∵在△BAD和△CAE中
 ,
,∴△BAD≌△CAE(SAS),
∴BD=CE;
②证明:∵△BAD≌△CAE,

∴∠AEC=∠ADB,
∵∠EAD=90°,
∴∠1+∠AEC=90°,
∵∠1=∠2,
∴∠2+∠ADB=90°,
∴∠DME=180°-90°=90°,
∴BD⊥CE;
③解:当三角形ABC绕点A顺时针方向旋转到如图②的位置时,上述结论还成立,
理由是:延长DB交CE于F,
∵在△BAD和△CAE中
 ,
,∴△BAD≌△CAE(SAS),
∴BD=CE,∠AEC=∠ADB,
∵∠EAD=90°,
∴∠4+∠ADB=90°,
∵∠3=∠4,
∴∠3+∠AEC=90°,
∴∠5=180°-90°=90°,
∴BD⊥CE,
即当三角形ABC绕点A顺时针方向旋转到如图②的位置时,上述结论还成立.
分析:①根据直角三角形性质得出∠BAC=∠EAD=90°,推出∠BAD=∠EAC,根据SAS证△BAD≌△CAE,推出BD=CE即可;
②根据全等三角形的性质推出∠AEC=∠ADB,根据∠1+∠AEC=90°推出∠2+∠ADB=90°,求出∠DME=90°,根据垂直定义求出即可;
③延长DB交CE于F,根据SAS证△BAD≌△CAE,推出BD=CE,∠AEC=∠ADB,求出∠3+∠AEC=90°,求出∠5=90°,根据垂直定义求出即可.
点评:本题考查了全等三角形的性质和判定,垂直定义,三角形的内角和定理等知识点,通过做此题培养了学生的猜想能力和推理能力,题目具有一定的代表性,是一道比较好的题目.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
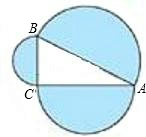 如图,在直角三角形ABC中,∠C=90°,AB=4,阴影部分的面积为( )
如图,在直角三角形ABC中,∠C=90°,AB=4,阴影部分的面积为( )| A、2π | B、3π | C、4π | D、6π |
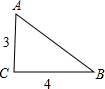
 如图,在直角三角形中,一直角边比另一直角边长1,且斜边长为5.
如图,在直角三角形中,一直角边比另一直角边长1,且斜边长为5.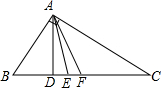 如图,在直角三角形ABC中,AD为斜边上的垂线,AE为角平分线,AF为中线,
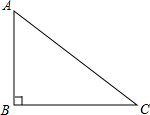
如图,在直角三角形ABC中,AD为斜边上的垂线,AE为角平分线,AF为中线,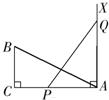 9、如图,在直角三角形ABC中,∠C=90°,AC=10cm,BC=5cm,一条线段PQ=AB,P、Q两点分别在AC和AC的垂线AX上移动,则当AP=
9、如图,在直角三角形ABC中,∠C=90°,AC=10cm,BC=5cm,一条线段PQ=AB,P、Q两点分别在AC和AC的垂线AX上移动,则当AP=