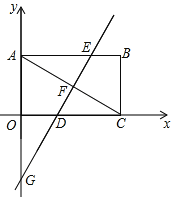
题目内容
【题目】如图,在平面直角坐标系中,抛物线经过![]() ,
,![]()
![]() ,⊙M是△ABC的外接圆,M为圆心.
,⊙M是△ABC的外接圆,M为圆心.
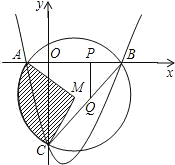
(1)求抛物线的解析式;
(2)求阴影部分的面积;
(3)在正半轴上有一点P,作PQ⊥x轴交BC于Q,设PQ=k,△CPQ的面积为S,求S关于k的函数关系式,并求出S的最大值.
【答案】(1)![]() ;(2)
;(2)![]() ;(3)
;(3)![]() ,
,![]() .
.
【解析】
试题分析:
(1)已知了A、B、C三点坐标可用待定系数法求出抛物线的解析式.
(2)要求扇形的面积需要知道半径的长和扇形的圆心角的度数,先求圆心角∠AMC的度数,由于OB=OC,因此∠ABC=45°,根据圆周角定理可得出∠AMC=90°.再求半径,由于三角形AMC是等腰直角三角形,因此半径的平方等于AC的平方的一半,可在直角三角形OAC中求出AC的平方,据此可根据扇形的面积公式求出扇形的面积.
(3)求三角形CPQ的面积可以PQ为底,以OP为高,已知了PQ=k,在等腰直角三角形BPQ中,BP=PQ=k,也就能表示长OP的长,据此可求出S与k的函数关系,根据函数的性质即可求出S的最大值.
试题解析:
解:(1)由抛物线经过![]() ,
,
设抛物线的解析式为:![]() ,
,
将![]() 代入上式中,得
代入上式中,得![]() .
.
∴![]() .
.
(2)∵![]() .
.
∴![]()
∴![]() ,∴
,∴![]()
∴![]()
∴![]() ,
,
∴![]() .
.
(3)![]() ,
,![]() 轴;
轴;
∴![]() ,
,
∴![]() .
.
∴当![]() 时,
时,![]() .
.
考点: 二次函数综合题.

练习册系列答案
相关题目