题目内容
 如图,已知点P是边长为5的正方形ABCD内的一点,连结PA,PB,PC,若PA=2,PB=4,∠APB=135°.
如图,已知点P是边长为5的正方形ABCD内的一点,连结PA,PB,PC,若PA=2,PB=4,∠APB=135°.(1)将△PAB绕点B顺时针旋转90°,画出△P′CB的位置.
(2)①求PC的长;
②求△PAB旋转到△P′CB的过程中边PA所扫过区域的面积.
分析:(1)利用旋转的性质得出对应点P′的位置进而得出即可;
(2)①利用旋转的性质得出,∠PP′C=90°,利用勾股定理得出PC的长;
②根据PA所扫过区域的面积为:S扇形ABC+S△BCP′-S扇形PBP′-S△ABP,进而得出即可.
(2)①利用旋转的性质得出,∠PP′C=90°,利用勾股定理得出PC的长;
②根据PA所扫过区域的面积为:S扇形ABC+S△BCP′-S扇形PBP′-S△ABP,进而得出即可.
解答: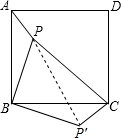 解:(1)如图所示:△P′CB即为所求;
解:(1)如图所示:△P′CB即为所求;
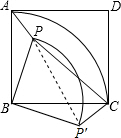
(2)①连接PP′,
∵将△PAB绕点B顺时针旋转90°,
∴PB=P′B=4,A,P,P′在一条直线上,∠PP′C=∠BP'C-∠BP'P=135°-45°=90°,
∵∠APB=135°,
∴∠BPP′=45°,
∴△PBP′是等腰直角三角形,
∴PP′=4
,
∵P′C=PC=2,
∴PC=
=6;
②△PAB旋转到△P′CB的过程中边PA所扫过区域的面积为:
S扇形ABC+S△BCP′-S扇形PBP′-S△ABP=S扇形ABC-S扇形PBP′=
=
π.
 解:(1)如图所示:△P′CB即为所求;
解:(1)如图所示:△P′CB即为所求;(2)①连接PP′,
∵将△PAB绕点B顺时针旋转90°,
∴PB=P′B=4,A,P,P′在一条直线上,∠PP′C=∠BP'C-∠BP'P=135°-45°=90°,
∵∠APB=135°,
∴∠BPP′=45°,
∴△PBP′是等腰直角三角形,
∴PP′=4
| 2 |

∵P′C=PC=2,
∴PC=
(4
|
②△PAB旋转到△P′CB的过程中边PA所扫过区域的面积为:
S扇形ABC+S△BCP′-S扇形PBP′-S△ABP=S扇形ABC-S扇形PBP′=
| 90π(52-42) |
| 360 |
| 9 |
| 4 |
点评:此题主要考查了旋转的性质以及旋转图形的画法和扇形面积公式等知识,根据题意得出旋转后图形的形状是解题关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
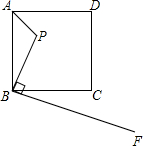 如图,已知点P是边长为5的正方形ABCD内一点,且PB=3,BF⊥BP于B,若在射线BF上找一点M,使以点B,M,C为顶点的三角形与△ABP相似,BM的值为( )
如图,已知点P是边长为5的正方形ABCD内一点,且PB=3,BF⊥BP于B,若在射线BF上找一点M,使以点B,M,C为顶点的三角形与△ABP相似,BM的值为( )| A、3 | ||
B、
| ||
C、3或
| ||
| D、3或5 |
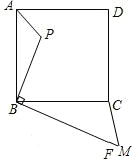 如图,已知点P是边长为4的正方形ABCD内的一点,且PB=3,BF⊥BP,若在射线BF有一点M,使以点B,M,C为顶点的三角形与△ABP相似,那么BM=
如图,已知点P是边长为4的正方形ABCD内的一点,且PB=3,BF⊥BP,若在射线BF有一点M,使以点B,M,C为顶点的三角形与△ABP相似,那么BM= 21、如图,已知点P是边长为4的正方形ABCD内一点,且PB=3,BF⊥BP,垂足是B.
21、如图,已知点P是边长为4的正方形ABCD内一点,且PB=3,BF⊥BP,垂足是B.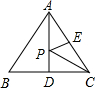 如图,已知点P是边长为2的正三角形ABC的中线AD上的动点,E是AC边的中点,则PC+PE的最小值是
如图,已知点P是边长为2的正三角形ABC的中线AD上的动点,E是AC边的中点,则PC+PE的最小值是