题目内容
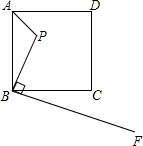如图，已知点P是边长为5的正方形ABCD内一点，且PB=3，BF⊥BP于B，若在射线BF上找一点M，使以点B，M，C为顶点的三角形与△ABP相似，BM的值为（ ）| A、3 | ||
B、
| ||
C、3或
| ||
| D、3或5 |
分析：由于∠ABC=∠PBF=90°，同时减去∠PBC后可得到∠ABP=∠CBF，若以点B，M，C为顶点的三角形与△ABP相似，那么必有：AB：PB=BC：BM或AB：BP=BM：BC，可据此求得BM的值．
解答：解：∵四边形ABCD是正方形，
∴∠ABC=90°，AB=BC=5；
又∵∠PBF=90°，
∴∠ABP=∠CBF=90°-∠CBP；
若以点B，M，C为顶点的三角形与△ABP相似，
则：①
=
，即
=
，解得BM=
；
②
=
，即
=
，解得BM=3；
故选C．
∴∠ABC=90°，AB=BC=5；
又∵∠PBF=90°，
∴∠ABP=∠CBF=90°-∠CBP；
若以点B，M，C为顶点的三角形与△ABP相似，
则：①
| AB |
| PB |
| BM |
| BC |
| 5 |
| 3 |
| BM |
| 5 |
| 25 |
| 3 |
②
| AB |
| BP |
| BC |
| BM |
| 5 |
| 3 |
| 5 |
| BM |
故选C．
点评：此题主要考查的是相似三角形的判定和性质，应注意相似三角形的对应顶点不明确时，要分类讨论，不要漏解．
练习册系列答案
相关题目
如图，已知点P是边长为4的正方形ABCD内的一点，且PB=3，BF⊥BP，若在射线BF有一点M，使以点B，M，C为顶点的三角形与△ABP相似，那么BM=
21、如图，已知点P是边长为4的正方形ABCD内一点，且PB=3，BF⊥BP，垂足是B．
如图，已知点P是边长为5的正方形ABCD内的一点，连结PA，PB，PC，若PA=2，PB=4，∠APB=135°．
如图，已知点P是边长为2的正三角形ABC的中线AD上的动点，E是AC边的中点，则PC+PE的最小值是